
题目列表(包括答案和解析)
(本小题满分14分)已知函数![]() 满足:
满足:![]() ;(1)分别写出
;(1)分别写出![]() 时
时![]() 的解析式
的解析式![]() 和
和![]() 时
时![]() 的解析式
的解析式![]() ;并猜想
;并猜想![]() 时
时![]() 的解析式
的解析式![]() (用
(用![]() 和
和![]() 表示)(不必证明)(2分)(2)当
表示)(不必证明)(2分)(2)当![]()
![]() 时,
时,![]()
![]() 的图象上有点列
的图象上有点列![]() 和点列
和点列![]() ,线段
,线段![]() 与线段
与线段![]() 的交点
的交点![]() ,求点
,求点![]() 的坐标
的坐标![]() ;(4分)
;(4分)
(3)在前面(1)(2)的基础上,请你提出一个点列![]() 的问题,并进行研究,并写下你研究的过程 (8分)
的问题,并进行研究,并写下你研究的过程 (8分)
(本小题满分14分) 已知函数![]() 及正整数数列
及正整数数列![]() . 若
. 若![]() ,且当
,且当![]() 时,有
时,有![]() ; 又
; 又![]() ,
,![]() ,且
,且![]() 对任意
对任意![]() 恒成立. 数列
恒成立. 数列![]() 满足:
满足:![]() .
.
(1) 求数列![]() 及
及![]() 的通项公式;
的通项公式;
(2) 求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3) 证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
(本小题满分14分)
将数列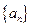 中的所有项按每一行比上一行多一项的规则排成如下数表
中的所有项按每一行比上一行多一项的规则排成如下数表 :
: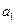
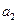
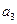
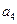
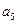
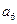
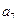
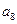
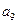
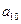
………………………
记表中的第一列数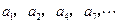 构成的数列为
构成的数列为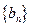 ,
,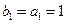 .
.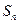 为数列
为数列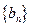 的前
的前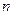 项和,且满足
项和,且满足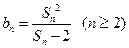 .
.
(1)证明: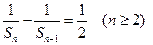 ;
;
(2)求数列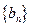 的通项公式;
的通项公式;
(3)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当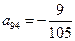 时,求上表中第
时,求上表中第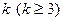 行所有项的和.
行所有项的和.
(本小题满分14分)
已知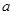 为实数,数列
为实数,数列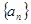 满足
满足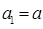 ,当
,当 时,
时,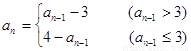
(1)当 时,求数列
时,求数列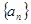 的前100项的和
的前100项的和 ;
;
(2)证明:对于数列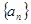 ,一定存在
,一定存在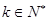 ,使
,使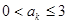 ;
;
(3)令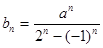 ,当
,当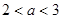 时,求证:
时,求证: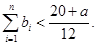
(本小题满分14分)
已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体, 存在非零常数
的全体, 存在非零常数 , 对任意
, 对任意 , 有
, 有 成立.
成立.
(1) 函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(2) 设 , 且
, 且 , 已知当
, 已知当 时,
时,  ,
求当
,
求当 时,
时,  的解析式.
的解析式.
(3)若函数 ,求实数
,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com