
题目列表(包括答案和解析)
(本小题满分10分)(注意:在试题卷上作答无效)
已知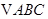 的内角A,B及其对边
的内角A,B及其对边 ,
,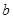 满足
满足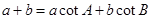 ,求内角
,求内角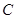 .
.
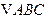 的内角A,B及其对边
的内角A,B及其对边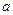 ,
,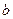 满足
满足 ,求内角
,求内角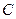 .
.(本小题满分10分)(注意:在试题卷上作答无效)
已知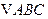 的内角A,B及其对边
的内角A,B及其对边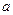 ,
,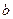 满足
满足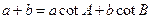 ,求内角
,求内角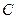 .
.
(本小题满分10分)(注意:在试题卷上作答无效) 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量
 且
且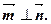
(Ⅰ)求 的大小;
的大小;
(Ⅱ)现给出下列四个条件:① ②
② ③
③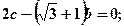 ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 ,求出你所确定的
,求出你所确定的 的面积.
的面积.
(本小题满分10分)(注意:在试题卷上作答无效)
 的三个内角A,B,C所对的边分别为a,b,c,
向量
的三个内角A,B,C所对的边分别为a,b,c,
向量
 且
且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)现给出下列四个条件:① ②
② ③
③ ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 ,求出你所确定的
,求出你所确定的 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com