
题目列表(包括答案和解析)
某地今年年初有居民住房面积为am2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
(1)如果10年后该地的人均住房面积正好比目前翻一番,那么每年应拆除的旧住房面积x是多少?
(2)依照(1)拆房速度,共需多少年能拆除所有需要拆除的旧住房?
下列数据供计算时参考:

| |||||||||||
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 90.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.6 | 173.0 |
已知 ,设
,设
 和
和 是方程
是方程 的两个根,不等式
的两个根,不等式 对任意实数
对任意实数 恒成立;
恒成立; 函数
函数 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数 的取值范围.
的取值范围.
【解析】本试题主要考查了命题和函数零点的运用。由题设x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
当a∈[1,2]时, 的最小值为3. 当a∈[1,2]时,
的最小值为3. 当a∈[1,2]时, 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
可得到要使“P∧Q”为真命题,只需P真Q真即可。
解:由题设x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
当a∈[1,2]时, 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
综上,要使“P∧Q”为真命题,只需P真Q真,即
解得实数m的取值范围是(4,8]
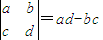 ,设
,设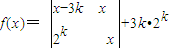 (x∈R,k为正整数)
(x∈R,k为正整数)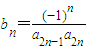 ,求数列{bn}的前n项和Tn的最大值.
,求数列{bn}的前n项和Tn的最大值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com