
题目列表(包括答案和解析)
已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当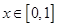 时,
时,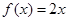 ,且在
,且在 内,关于
内,关于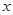 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是
已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当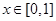 时,
时,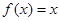 ,那么在区间
,那么在区间 内,关于
内,关于 的方程
的方程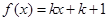 (其中
(其中 走为不等于l的实数)有四个不同的实根,则
走为不等于l的实数)有四个不同的实根,则 的取值范围是( )
的取值范围是( )
A. B.
B.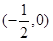 C.
C.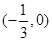 D.
D.
已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是
 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是 已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,那么在区间
,那么在区间 内,关于
内,关于 的方程
的方程 (其中
(其中 走为不等于l的实数)有四个不同的实根,则
走为不等于l的实数)有四个不同的实根,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com