
题目列表(包括答案和解析)
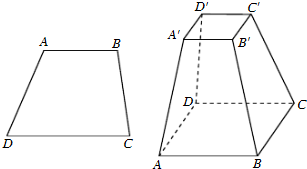 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.| x |
| x+h |
| a |
| b |
| ah |
| b-a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| h |
| y-a |
| b-a |
| b-a |
| h |
| ∫ | h 0 |
| b-a |
| h |
| b-a |
| 2h |
| | | h 0 |
| b-a |
| 2h |
| 1 |
| 2 |
| 1 |
| 3 |
 用长为16米的篱笆借助一墙角围成一个矩形ABCD(如图所示),在P处有一棵树距两墙的距离分别为a(0<a<12)米和4米,现需要将此树圈进去,设矩形ABCD的面积为y(平方米),长BC为x(米).
用长为16米的篱笆借助一墙角围成一个矩形ABCD(如图所示),在P处有一棵树距两墙的距离分别为a(0<a<12)米和4米,现需要将此树圈进去,设矩形ABCD的面积为y(平方米),长BC为x(米).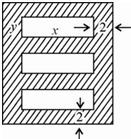 为了美化校园环境,学校打算在兰蕙广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为x,宽为y,整个矩形花园面积为S.
为了美化校园环境,学校打算在兰蕙广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为x,宽为y,整个矩形花园面积为S.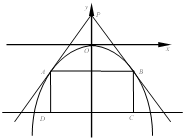 如图,过点P(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,且AD和BC均垂直于直线y=-8,垂足分别为D,C,得矩形ABCD.
如图,过点P(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,且AD和BC均垂直于直线y=-8,垂足分别为D,C,得矩形ABCD.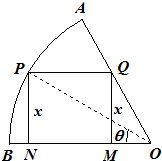 如图,在半径为
如图,在半径为| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com