
题目列表(包括答案和解析)
| π |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
(1)所有在N中的元素都在N*中;( )
(2)所有在N中的元素都在Z中;( )
(3)所有不在N*中的数都不在Z中;( )
(4)所有不在Q中的实数都在R中;( )
(5)由既在R中又在N*中的数组成的集合中一定包含数0;( )
(6)不在N中的数不能使方程4x=8成立.( )
有4男3女共7位同学从前到后排成一列.
(1)有多少种不同方法?
(2)甲不站在排头,有多少种不同方法?
(3)三名女生互不相邻,有多少种不同方法?
(4)3名女生在队伍中按从前到后从高到矮顺序排列,有多少种不同方法?
(5)3名女生必须站在一起,有多少种不同方法?
(本小题满分10分)
(1)在等差数列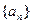 中,d=2,n=15,
中,d=2,n=15,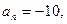 求
求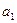 及
及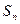
(2) )在等比数列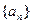 中,
中,
 求
求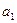 及q.
及q.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com