
题目列表(包括答案和解析)
(本小题满分12分)
如图,台风中心从A地以每小时20千米的速度向东北方向(北偏东 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题: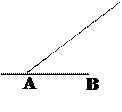
(1) 求台风移动路径所在的直线方程;
(2)求城市B处于危险区域的时间是多少小时?
(本小题满分12分)
如图,台风中心从A地以每小时20千米的速度向东北方向(北偏东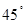 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
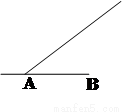
(1) 求台风移动路径所在的直线方程;
(2)求城市B处于危险区域的时间是多少小时?
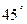 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题: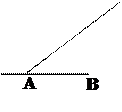
 ,
, 
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)若关于 的不等式
的不等式 存在实数解,则实数
存在实数解,则实数 的取值范围是
.
的取值范围是
.
 B.(几何证明选做题)如图,∠B=∠D,
B.(几何证明选做题)如图,∠B=∠D, ,
, ,且AB=6,AC=4,AD=12,则BE= .
,且AB=6,AC=4,AD=12,则BE= .
C.(坐标系与参数方程选做题)直角坐标系 中,以原点O为极点,
中,以原点O为极点, 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线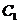 :
: (
( 为参数)和曲线
为参数)和曲线 :
: 上,则
上,则 的最小值为
.
的最小值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com