（04年北京卷文）(14分)

函数f(x)定义在[0,1]上,满足且f(1)=1,在每个区间=1,2,…)上, y=f(x) 的图象都是平行于x轴的直线的一部分.

(Ⅰ)求f(0)及的值,并归纳出)的表达式;

(Ⅱ)设直线轴及y=f(x)的图象围成的矩形的面积为, 求a₁,a₂及的值.

(本小题满分14分)函数f(x)＝1－2a－2acosx－2sin²x的最小值为g(a)(a∈R)．

(1)求g(a)；

(2)若g(a)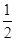＝，求a及此时f(x)的最大值．

(本小题14分)

函数f(x)对任意的a、b∈R,都有f(a+b)=f(a)+f(b)-1,

并且当x＞0时，f(x)＞1.

（1）求证：f(x)是R上的增函数；

（2）若f(4)=5,解不等式f(3m²-m-2)＜3.

（本小题满分14分）

f(x)是定义在R上的奇函数，且，当时，

（1）求函数的周期   （2）求函数在的表达式 （3）求

（01全国卷理）(14分)

设f (x) 是定义在R上的偶函数，其图像关于直线x = 1对称．对任意x₁，x₂∈[0，]都有f (x₁＋x₂) = f (x₁) ? f (x₂)．且f (1) = a＞0．

    (Ⅰ)求f () 及f ()；

(Ⅱ)证明f (x) 是周期函数；

(Ⅲ)记a_n = f (2n＋)，求．