
题目列表(包括答案和解析)
(2012年高考江苏卷19) (本小题满分16分)
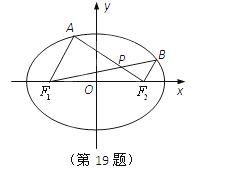 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .已知
.已知![]() 和
和![]() 都在椭圆上,其中e为椭圆的离心率.
都在椭圆上,其中e为椭圆的离心率.
(1)求椭圆的离心率;
(2)设A,B是椭圆上位于x轴上方的两点,且直线![]()
与直线![]() 平行,
平行,![]() 与
与![]() 交于点P.
交于点P.
(i)若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(ii)求证:![]() 是定值.
是定值.
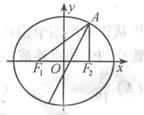 (2010安徽理数)19、(本小题满分13分)
(2010安徽理数)19、(本小题满分13分)
已知椭圆![]() 经过点
经过点![]() ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点
![]() 在
在![]() 轴上,离心率
轴上,离心率![]() 。
。
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的角平分线所在直线
的角平分线所在直线![]() 的方程;
的方程;
(Ⅲ)在椭圆![]() 上是否存在关于直线
上是否存在关于直线![]() 对称的相异两点?
对称的相异两点?
若存在,请找出;若不存在,说明理由。
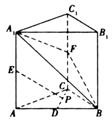
(本小题满分12分)如图所示,在直三棱柱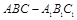 中,
中,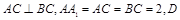 、
、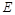 、
、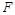 分别是
分别是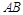 、
、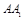 、
、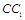 的中点,
的中点,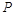 是
是 上的点.
上的点.
(1)求直线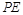 与平面
与平面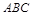 所成角的正切值的最大值;
所成角的正切值的最大值;
(2)求证:直线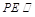 平面
平面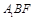 ;
;
(3)求直线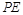 与平面
与平面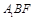 的距离.
的距离.
|
. 19(本小题满分14分)
 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线
x+y-1 = 0相交于A、B两点,且OA⊥OB
(O为坐标原点).
(I) 求 + 的值;
(II) 若椭圆长轴长的取值范围是[,],
求椭圆离心率e的取值范围.
(本小题满分12分)
在清明节前,哈市某单位组织员工参加植树祭扫,林管局在植树前为了保证树苗质量,都会对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,量出它们的高度如下:(单位:厘米)
甲:37 21 31 21 28 19 32 23 25 33
乙:10 30 47 27 46 14 26 11 43 46
(1)根据抽测结果画出茎叶图,并根据你所填写的茎叶图对两种树苗高度作比较,写出3个统计结论;
(2)如果认为甲种树苗高度超过30厘米为优质树苗,那么在己抽测的甲种10株树苗中任选两株栽种,记优质树苗的个数为 ,求
,求 的分布列和期望.
的分布列和期望.
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.答案:A
解:依题意可知:由
 显然:
显然: 但
但 不能推出
不能推出 。
。
故选A ;
2.答案:D
解:依题意可知:设点 ,则在点P处的切线的斜率为
,则在点P处的切线的斜率为 ,即
,即 ,又
,又
故选D ;
3.答案:C
解:依题意可知:由 是奇函数,
是奇函数,


故选C ;
4.答案:A
解:依题意可知:由


故选A;
 5.答案:C
5.答案:C
解:如图:函数 是周期函数,T=1。
是周期函数,T=1。
故选C;
6.答案:A
解:依题意可知:由
 ,
,
 ,
,
又
 。
。
故选A ;
 7.答案:B
7.答案:B
解:依题意可知:由图可知:
 。
。
8.答案:A
解:依题意可知:如图,

 ,
,
则在 中,
中, ;
;
则在 中,
中, ;
;
则在 中,
中, ;
;
故选A ;
9.答案:D
解:依题意可知:因 表示与
表示与 同方向的单位向量,
同方向的单位向量,
 表示与
表示与 同方向的单位向量,故
同方向的单位向量,故
 ,而
,而



 ,
,
又( +
+ )
) ,说明
,说明 向量与
向量与 向量垂直,根据向量加法的平行四边形法则可知:
向量垂直,根据向量加法的平行四边形法则可知: 向量所在直线 过
向量所在直线 过 向量所在线段中点,根据等腰三角形三线合一的性质,可逆推
向量所在线段中点,根据等腰三角形三线合一的性质,可逆推 为等腰三角形。又
为等腰三角形。又 与
与 夹角为
夹角为 ,故
,故 为等边三角形。
为等边三角形。
故选D ;
10.答案:A
解:设 ,在
,在
 上,
上, ,
, ,
, ,排除D;在
,排除D;在
 上,
上, ,
, ,
, ,排除B与C;故选A。
,排除B与C;故选A。
11.答案:B
解法一:正方体的八个顶点可确定 条直线;
条直线; 条直线组成
条直线组成 对直线;正方体的八个顶点可确定
对直线;正方体的八个顶点可确定 个面,其中12个四点面(6个表面,4个面对角面,2个体对角面),8个三点面;每个四点面上有
个面,其中12个四点面(6个表面,4个面对角面,2个体对角面),8个三点面;每个四点面上有 条直线,6条直线组成
条直线,6条直线组成 对直线,12个四点面由12×15=180对直线组成;每个三点面上有
对直线,12个四点面由12×15=180对直线组成;每个三点面上有 条直线,3条直线组成
条直线,3条直线组成 对直线,8个三点面由8×3=24对直线组成;由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为
对直线,8个三点面由8×3=24对直线组成;由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为 ;
;
解法二:正方体的八个顶点可确定 个四面体,每个四面体中有三对异面直线,由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为
个四面体,每个四面体中有三对异面直线,由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为 ;
;
12.答案:A
解:①正确;①中依题意可令 ,
,
当 时,
时,
 在
在 上为减函数,
上为减函数,
又因 在区间
在区间 为减函数,故
为减函数,故 ;
;
②错误;②中 当
当
当
③错误;③中当 时,
时,
④正确;
 圆的对称轴为直径所在的直线,故原命题正确。
圆的对称轴为直径所在的直线,故原命题正确。
故答案为:A。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上。
13.答案:
解:设P点的坐标为 ,则
,则
 直线PQ的方程为:
直线PQ的方程为: 即
即 ,
,
 Q点的坐标为
Q点的坐标为 ,R点的坐标为
,R点的坐标为 ,
,


故答案为: ;
;
14.答案:
解:依题意可知:正四棱锥S―ABCD的底面正方形ABCD在过球心O的大圆上,设球半径为R,AC=2R= ,
,
 ;
;
设球心O到侧面SAB的距离为 ,连接
,连接
 ,
, ,过
,过 作
作 于
于 ,
,
连接SM,则 ,
,


 ,
,
又 4
4 。
。
故答案为: ;
;
15.答案:10
解:依题意可知:由 令
令 ,故
,故 的系数为
的系数为 。
。
故答案为:10 ;
16.答案:③
解:依题意可知:①错,因在 上,
上, 为减函数,而在
为减函数,而在 上,
上, 为增函数。
为增函数。
②错,因在 上,
上, 为增函数,而在
为增函数,而在 上,
上, 为减函数。
为减函数。
③正确。因在 上,
上, 为增函数。
为增函数。
④错,因在 上,
上, 为增函数,而在
为增函数,而在 上,
上, 为减函数,故
为减函数,故 时,函数
时,函数 有极大值。
有极大值。
⑤错,因在 上,
上, 为增函数,故
为增函数,故 时,函数
时,函数 没有极大值。
没有极大值。
故答案为:③;
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
(17)解: ,设
,设 中有
中有 个元素,显然有
个元素,显然有 ,其中最大的一个是
,其中最大的一个是 ,由于
,由于 是正整数集合,故
是正整数集合,故 且
且 ;
;
当 时,
时, ,此时不符合题意;
,此时不符合题意;
当 时,
时, 或
或 或
或 ,显然只有
,显然只有 符合题意;
符合题意;
当 时,设
时,设 其中
其中 ,
,
此时令
 ,
,
若 ,则
,则
 ,
,
 不符合题意;
不符合题意;
若 ,由于
,由于 是正整数集合,故
是正整数集合,故 ,
,


 故
故 时不符合题意;
时不符合题意;
综上所述 。
。
(18)解:令


故当
 (19)。答:与平面
(19)。答:与平面 垂直的直线条数有1条为
垂直的直线条数有1条为 ;
;
证法一:依题意由图可知:连 ,
,

连 ,
,
 ;
;
证法二:依题意由图建立空间直角坐标系:

 ,
,
设与 垂直的法向量为
垂直的法向量为 ,则有:
,则有:

 ,而
,而 ,故
,故 。
。
(20)解:设S为劳动村全体农民的集合, 为
为 季度劳动村在外打工的农民的集合,则
季度劳动村在外打工的农民的集合,则 为
为 季度劳动村没有在外打工的农民的集合,由题意有
季度劳动村没有在外打工的农民的集合,由题意有

所以
劳动村的农民全年在外打工为 ,则
,则

 ,
,
但
 ,
,
所以
 ,
,
即
 。
。
故劳动村至少有 的农民全年在外打工。
的农民全年在外打工。
(21)解:①作图进行受力分析,如下图示;
由向量的平行四边形法则,力的平衡及解直角三角形等知识,得出:


② ∵
 ,∴
,∴
故 在
在 上为减函数,
上为减函数,
∴当 逐渐增大时,
逐渐增大时, 也逐渐增大。
也逐渐增大。
③要 最小,则
最小,则 为最大,∴当
为最大,∴当 为
为 时,
时, 最小,最小值是
最小,最小值是 。
。
④要 ,则
,则 ,∴当
,∴当 为
为 时,
时, 。
。
(22)解:(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为
将 代入方程
代入方程 ,并整理得
,并整理得 
设 则有
则有 



所以 夹角的大小为
夹角的大小为
(Ⅱ)由题设 得
得 
|