已知抛物线C：y²=2px（p＞0）上任意一点到焦点F的距离比到y轴的距离大1．
（1）求抛物线C的方程；
（2）若过焦点F的直线交抛物线于M、N两点，M在第一象限，且|MF|=2|NF|，求直线MN的方程；
（3）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题．
例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”．求出体积后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为，求侧棱长”；也可以是“若正四棱锥的体积为，求所有侧面面积之和的最小值”．
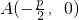现有正确命题：过点的直线交抛物线C：y²=2px（p＞0）于P、Q两点，设点P关于x轴的对称点为R，则直线RQ必过焦点F．
试给出上述命题的“逆向”问题，并解答你所给出的“逆向”问题．

已知抛物线上任意一点到焦点F的距离比到轴的距离大1，（1）求抛物线C的方程；（2）若过焦点F的直线交抛物线于M，N两点，M在第一象限，且，求直线MN的方程；（3）过点的直线交抛物线于P、Q两点，设点P关于轴的对称点为R，求证：直线RQ必过定点．