已知直三棱柱中, , ， 是和的交点, 若.

（1）求的长；  （2）求点到平面的距离；

（3）求二面角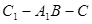的平面角的正弦值的大小.

【解析】本试题主要考查了距离和角的求解运用。第一问中，利用ACCA为正方形, AC=3

第二问中，利用面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD=，第三问中，利用三垂线定理作二面角的平面角，然后利用直角三角形求解得到其正弦值为

解法一: (1)连AC交AC于E, 易证ACCA为正方形, AC=3 ……………  5分

(2)在面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD= … 8分

(3) 易得AC面ACB, 过E作EHAB于H, 连HC, 则HCAB

CHE为二面角C－AB－C的平面角. ………  9分

sinCHE=二面角C－AB－C的平面角的正弦大小为 ……… 12分

解法二: (1)分别以直线CB、CC、CA为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C(0, 0, 0), B(4, 0, 0), B(4, －3, 0), C(0, －3, 0), A(0, 0, h), A(0, －3, h), G(2, －, －) ………………………  3分

=(2, －, －), =(0, －3, －h)  ……… 4分

·=0,  h=3

(2)设平面ABC得法向量=(a, b, c),则可求得=(3, 4, 0) (令a=3)

点A到平面ABC的距离为H=||=……… 8分

(3) 设平面ABC的法向量为=(x, y, z),则可求得=(0, 1, 1) (令z=1)

二面角C－AB－C的大小满足cos== ………  11分

二面角C－AB－C的平面角的正弦大小为

如图，四棱锥P-ABCD中，底面ABCD为菱形，PA底面ABCD，AC=,PA=2，E是PC上的一点，PE=2EC。

（I）     证明PC平面BED；

（II）   设二面角A-PB-C为90°，求PD与平面PBC所成角的大小

【解析】本试题主要是考查了四棱锥中关于线面垂直的证明以及线面角的求解的运用。

从题中的线面垂直以及边长和特殊的菱形入手得到相应的垂直关系和长度，并加以证明和求解。

解法一：因为底面ABCD为菱形，所以BDAC,又

【点评】试题从命题的角度来看，整体上题目与我们平时练习的试题和相似，底面也是特殊的菱形，一个侧面垂直于底面的四棱锥问题，那么创新的地方就是点E的位置的选择是一般的三等分点，这样的解决对于学生来说就是比较有点难度的，因此最好使用空间直角坐标系解决该问题为好。

如图，四棱锥S—ABCD中，SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB

(Ⅰ)证明：平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小                .

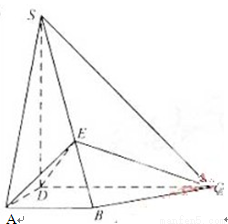
【解析】本试题主要考查了立体几何中的运用。

(1)证明：因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB   所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.，因此可知得到平面EDC⊥平面SBC.

（Ⅱ）由SA²= SD²+AD² = 5 ，AB=1，SE=2EB，AB⊥SA，知

AE²= (1 /3 SA)²+(2/ 3 AB)² =1，又AD=1．

故△ADE为等腰三角形．

取ED中点F，连接AF，则AF⊥DE，AF²= AD²-DF² =．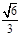

连接FG，则FG∥EC，FG⊥DE．

所以，∠AFG是二面角A-DE-C的平面角．

连接AG，AG= 2 ，FG²= DG²-DF² =，

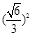cos∠AFG=(AF²+FG²-AG² )/2⋅AF⋅FG =-1 /2 ，

所以，二面角A-DE-C的大小为120°

已知三棱锥P—ABC中，PC⊥底面ABC，,，二面角P-AB-C为，D、F分别为AC、PC的中点，DE⊥AP于E．

（Ⅰ）求证：AP⊥平面BDE；                

（Ⅱ）求直线EB与平面PAC所成的角。

【解析】本试题主要考查了线面的垂直问题以及线面角的求解的综合运用。

零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分

【解析】（Ⅰ）解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P（A）==.

      （Ⅱ）（i）解：一等品零件的编号为.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,

,,,共有15种.

      (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”（记为事件B）的所有可能结果有：，，共有6种.

      所以P(B)=.

（本小题满分12分）

如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=，∠BAD＝∠CDA＝45°.

（Ⅰ）求异面直线CE与AF所成角的余弦值；      

（Ⅱ）证明CD⊥平面ABF；

（Ⅲ）求二面角B-EF-A的正切值。