
题目列表(包括答案和解析)
设a为实数, 函数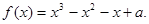
(Ⅰ)求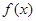 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线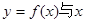 轴仅有一个交点.
轴仅有一个交点.
设a为实数, 函数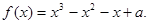
(Ⅰ)求 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线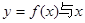 轴仅有一个交点.
轴仅有一个交点.
设a为实数,函数![]()
(Ⅰ)求![]() 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线![]() 轴仅有一个交点.
轴仅有一个交点.
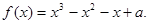
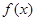 的极值.
的极值.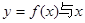 轴仅有一个交点.
轴仅有一个交点.设a为实数,函数![]()
(Ⅰ)求![]() 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线![]() 轴仅有一个交点.
轴仅有一个交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com