
题目列表(包括答案和解析)
①S1与S2;②a2与S3;③a1与an;④q与an.其中n为大于1的整数,Sn为{an}的前n项和.
①S1与S2;②a2与S3;③a1与an;④q与an中,一定能成为该数列“基本量”的是第_____________.其中n为大于1的整数,Sn为{an}的前n项和.
若干个能唯一确定一个数列的量称为该数列的“基本量”.设 是公比为
是公比为 的无穷等比数列,下列
的无穷等比数列,下列 的四组量中,一定能成为该数列“基本量”的是第 组;
的四组量中,一定能成为该数列“基本量”的是第 组;
① ;②
;② ;③
;③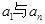 ;④
;④ .
.
若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是________.(写出所有符合要求的组号)
①S1与S2;②a2与S3;③a1与an;④q与an.其中n为大于1的整数,Sn为{an}的前n项和.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com