
题目列表(包括答案和解析)
①存在α∈(0, )使sin α+cos α=
)使sin α+cos α= ;
;
②存在区间(a,b)使y=cos x为减函数且sin x<0;
③y=tan x在其定义域内为增函数;
④y=cos 2x+sin( -x)既有最大、最小值,又是偶函数;
-x)既有最大、最小值,又是偶函数;
⑤y=|sin 2x+ |的最小正周期为π.
|的最小正周期为π.
以上命题错误的为________(填序号).
 使
使 ;
; 既有最大、最小值,又是偶函数;
既有最大、最小值,又是偶函数; 最小正周期为π.
最小正周期为π. 使
使 ;
; 既有最大、最小值,又是偶函数;
既有最大、最小值,又是偶函数; 最小正周期为π.
最小正周期为π. 使
使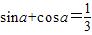 ;
; 既有最大、最小值,又是偶函数;
既有最大、最小值,又是偶函数; 最小正周期为π.
最小正周期为π. 使
使 ;
; 既有最大、最小值,又是偶函数;
既有最大、最小值,又是偶函数; 最小正周期为π.
最小正周期为π.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com