
题目列表(包括答案和解析)
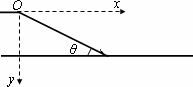
(平抛运动+运动的分解+功能关系或牛顿运动定律)倾斜雪道的长为25 m,顶端高为15 m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8 m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起.除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,求运动员在水平雪道上滑行的距离(取g=10 m/s2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com