
题目列表(包括答案和解析)
(14 分)如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
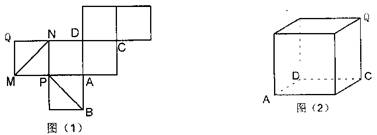
(1)求证:MN//平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P—DB—M 的大小.
(本小题共14分)
某学校餐厅新推出![]() 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
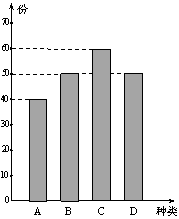
| 满意 | 一般 | 不满意 | |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中
的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
(本小题共14分)
某学校餐厅新推出![]() 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
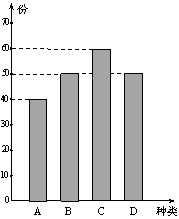
| 满意 | 一般 | 不满意 | |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中
的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
(本题是选做题,满分28分,请在下面四个题目中选两个作答,每小题14分,多做按前两题给分)
A.(选修4-1:几何证明选讲)
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
B.(选修4-2:矩阵与变换)
在直角坐标系中,已知椭圆 ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积.
C.(选修4-4:坐标系与参数方程)
直线 (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.
D.(选修4-5:不等式选讲)
设 ,求证:
,求证: .
.
 (本小题满分14分)某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(本小题满分14分)某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(I)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(II)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| 甲班 | 乙班 | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
![]()
|
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2. 706 | 3. 841 | 5. 024 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com