如右图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度随时间变化的图象可能是（    ）

 

                     

（一）必做题（11～13题）

查看答案和解析>>

查看答案和解析>>

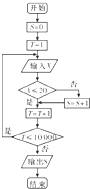（必做题）为调查长沙市中学生平均每人每天参加体育锻炼时间（单位：分钟），按锻炼时间分下一列四种情况统计：①0～10分钟；②11～20分钟；③21～30分钟；④30分钟以上．有l0 000名中学生参加了此项活动，如图是此次调查中某一项的流程图，其输出的结果是6 200，则平均每天参加体育锻炼时间在0～20分钟内的学生的频率是

 

．

查看答案和解析>>

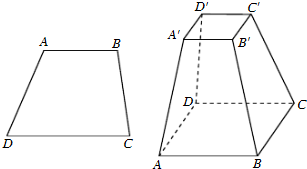（必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
设OE=x，∵△OAB∽△ODC，∴

x

x+h

=

a

b

，即x=

ah

b-a

．
∴S_梯形ABCD=S_△ODC-S_△OAB=

1

2

b（x+h）-

1

2

ax=

1

2

（b-a）x+

1

2

bh=

1

2

（a+b）h．
方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
设梯形AMNB的高为x，MN=y，

x

h

=

y-a

b-a

⇒y=a+

b-a

h

x，∴S梯形ABCD=

∫

h 0

（a+

b-a

h

x）dx=（ax+

b-a

2h

x²）

|

h 0

=ah+

b-a

2h

•h²=

1

2

（a+b）h．
再解下面的问题：
已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S₁，S₂（S₁＜S₂），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=

1

3

×底面积×高）．

查看答案和解析>>

查看答案和解析>>

一、选择题：本大题主要考查基本知识和基本运算.共10小题，每小题5分，

满分50分．

题号

1

2

3

4

5

6

7

8

9

10

答案

B

A

B

C

B

D

A

D

D

C

二、填空题：本大题主要考查基本知识和基本运算. 本大题共5小题，每小

题5分，满分20分．其中14～15题为选做题，考生只能选做一题. 第十二题的第一个空2分，第二个空3分．

11. ；    12. 1， 2^n-1；          13. 80；   14.；       15.1.

三、解答题：本大题共6小题，共80分．解答须写出文字说明、证明过程和演算步骤.

16.(本小题满分12分)

某校高三年级要从3名男生a、b、c和2名女生d、e中任选3名代表参加

学校的演讲比赛.

(1)求男生a被选中的概率； (2) 求男生a和女生d至少一人被选中的概率.

解：从3名男生a、b、c和2名女生d、e中任选3名代表选法是：

a，b，c；a，b，d；a，b，e；a，c，d；a，c，e；a，d，e；b，c，d；

b，c，e；b，d，e；c，d，e共10种.                    ……4分

(1)男生a被选中的选法是：a，b，c；a，b，d；a，b，e；a，c，d；a，c，e；a，d，e，共6种，于是男生a被选中的概率为.  ……8分

(2) 男生a和女生d至少一人被选中的选法是：a，b，c；a，b，d；a，b，e；a，c，d；a，c，e；a，d，e；b，c，d；b，d，e；c，d，e共9种，

故男生a和女生d至少一人被选中的概率为.           ……12分                            

17.(本小题满分14分)

已知△ABC的内角A、B、C所对的边分别为a，b，c，且a=2， cosB=．

(1)若b=4，求sinA的值； (2) 若△ABC的面积S_△ABC=4，求b，c的值．

解：(1) ∵cosB=>0，且0<B<π，

∴sinB=.                              ……2分

由正弦定理得，                          ……4分

 .                           ……6分

(2) ∵S_△ABC=acsinB=4，                             ……8分

 ∴，  ∴c=5.                      ……10分

由余弦定理得b²=a²+c²－2accosB，

∴.……14分

18.(本小题满分14分) 如图4，A₁A是圆柱的母线，AB是圆柱底面圆的直径， C是底面圆周上异于A，B的任意一点，A₁A= AB=2.

(1)求证: BC⊥平面A₁AC；

(2)求三棱锥A₁-ABC的体积的最大值.

证明:∵C是底面圆周上异于A，B的任意一点，

且AB是圆柱底面圆的直径，

∴BC⊥AC,                  ……2分

∵AA₁⊥平面ABC，BCÌ平面ABC，

∴AA₁⊥BC，                ……4分

∵AA₁∩AC=A，AA₁Ì平面AA₁ C，

ACÌ平面AA₁ C，

                            ∴BC⊥平面AA₁C.           ……6分

(2)解法1：设AC=x，在Rt△ABC中，

(0<x<2) ,                     ……7分

故(0<x<2),

……9分

即. ……11分

∵0<x<2，0<x²<4，∴当x²=2，即时，

三棱锥A₁-ABC的体积的最大值为.                       ……14分

解法2: 在Rt△ABC中，AC²+BC²=AB²=4，                  ……7分

                ……9分

.               ……11分

当且仅当 AC=BC 时等号成立，此时AC=BC=.

∴三棱锥A₁-ABC的体积的最大值为.                     ……14分

19. (本小题满分14分)

设A(x₁，x₂)、B(x₂，y₂)是抛物线x²=4y上不同的两点，且该抛物线在点A、B处的两条切线相交于点C，并且满足.

(1)求证：x_1?x₂=－4；

(2)判断抛物线x²=4y的准线与经过A、B、C三点的圆的位置关系，并说明理由.

(1) 证明：由x²=4y得，则，

∴抛物线x²=4y在点A(x₁，x₂)、B(x₂，y₂)处的切线的斜率分别为，

……2分

∵，∴，                            ……4分

∴抛物线x²=4y在点A(x₁，x₂)、B(x₂，y₂)处两切线互相垂直，

∴，∴x_1?x₂=－4.                             ……6分

(2) 解法1: ∵，∴，

∴经过A、B、C三点的圆的圆心为线段AB的中点D，

圆心D，                            ……8分

∵抛物线x²=4y的准线方程为y=－1, ∴点D到直线

y=－1的距离为，                       ……10分

∵经过A、B、C三点的圆的半径，

由于x₁²=4y₁，x₂²=4y₂，且x_1?x₂=－4，则，

∴

，

即

，                         ……12分

∴d=r，∴抛物线x²=4y准线与经过A、B、C三点的圆相切.  ……14分

解法2:由(1)知抛物线x²=4y在点A(x₁，x₂)处的切线的斜率为

又x₁²=4y₁，∴切线AC所在直线方程为，

即                              ①      ……8分

同理可得切线BC所在直线方程为  ②

由①，②得点C的横坐标，纵坐标y_C=－1，即

……10分

∵，∴，

∴经过A、B、C三点的圆的圆心为线段AB的中点D，

圆心D，

∵抛物线x²=4y的准线方程为y=－1,

∴点D到直线y=－1的距离为，            ……12分                 

∵经过A、B、C三点的圆的半径r=|CD|=，

∴d=r，∴抛物线x²=4y准线与经过A、B、C三点的圆相切.  ……14分

20. (本小题满分12分)

某车间有50名工人，要完成150件产品的生产任务，每件产品由3个A 型零件和1个B 型零件配套组成. 每个工人每小时能加工5个A 型零件或者3个B 型零件，现在把这些工人分成两组同时工作(分组后人数不再进行调整)，每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N^*)

(1)设完成A 型零件加工所需时间为f(x)小时，写出f(x)的解析式；

(2)为了在最短时间内完成全部生产任务，x应取何值？

(本题主要考查函数最值、不等式、导数及其应用等基础知识，考查分类与整合的数学思想方法，以及运算求解和应用意识)

解：(1) 生产150件产品，需加工A型零件450个，则完成A型零件加工所需时间(x∈N*，且1≤x≤49).              ……2分   

(2) 生产150件产品，需加工B型零件150个，则完成B型零件加工所需时间(x∈N*，且1≤x≤49).            ……4分设完成全部生产任务所需时间h(x)小时，则h(x)为f(x)与 g(x)的较大者，

令f(x)≥g(x)，则，解得，

所以，当1≤x≤32时，f(x)>g(x)；当33≤x≤492时，f(x)<g(x).

故                 ……6分

当1≤x≤32时，，故h(x)在[1，32]上单调递减，

则h(x)在[1，32]上的最小值为(小时)；       ……8分

当33≤x≤49时，，故h(x)在[33，49]上单调递增，

则h(x)在[33，49]上的最小值为(小时)； ……10分

∵h(33)> h(32)，∴h(x)在[1，49]上的最小值为h(32)， ∴x=32.

答：为了在最短时间内完成全部生产任务，x应取32.        ……12分

21. (本小题满分14分)

已知数列{a_n}的相邻两项a_n，a_n+1是关于x 的方程x²－2ⁿ x+ b_n=0 (n∈N^*)的两根，且a₁=1.

(1)求证：数列{ a_n－×2ⁿ}是等比数列；

(2)设S_n是数列{a_n}的前n项的和，问是否存在常数λ，使得b_n－λS_n>0对任意n∈N^*都成立，若存在，求出λ的取值范围；若不存在，请说明理由.     

(本题主要考查数列的通项公式、数列前n项和、不等式等基础知识，考查化归与转化、分类与整合、特殊与一般的数学思想方法，以及推理论证能力、运算求解能力和抽象概括能力)

(1)证法1：∵a_n，a_n+1是关于x 的方程x²－2ⁿ x+ b_n=0 (n∈N^*)的两根，

∴                                        ……2分

由a_n+a_n+1=2ⁿ，得，故数列

是首项为，公比为－1的等比数列.                 ……4分

证法2：∵a_n，a_n+1是关于x 的方程x²－2ⁿ x+ b_n=0 (n∈N^*)的两根，

∴                                        ……2分

∵，

故数列是首项为，公比为－1的等比数列.             

   ……4分

(2)解：由(1)得，即，

∴

                             ……6分

∴S_n=a₁+ a₂+ a₃+…+ a_n=[(2+2²+2³+…+2ⁿ)－[(－1)+ (－1)²+…+(－1)ⁿ]

，                        ……8分

要使得b_n－λS_n>0对任意n∈N^*都成立，

即对任意n∈N*都成立.

①当n为正奇数时，由(*)式得，

即，

∵2ⁿ⁺¹－1>0，∴对任意正奇数n都成立.

当且仅当n=1时，有最小值1，∴λ<1.           ……10分

①当n为正奇数时，由(*)式得，

即，

∵2ⁿ⁺¹－1>0，∴对任意正奇数n都成立.

当且仅当n=1时，有最小值1，∴λ<1.           ……10分

②当n为正偶数时，由(*)式得，

即，

∵2ⁿ－1>0，∴对任意正偶数n都成立.

当且仅当n=2时，有最小值1.5，∴λ<1.5.      ……12分

综上所述，存在常数λ，使得b_n－λS_n>0对任意n∈N^*都成立，λ的取值范围是(－∞，1).                                            ……14分