
题目列表(包括答案和解析)
如图所示,在距水平地面一定高度处以初速度v0水平抛出一个质量为m、电荷量为Q的带正电的小球.当小球运动的空间范围内不存在电场和磁场时,小球的落地点与抛出点之间有相应的一段水平距离(即射程),已知重力加速度为g.
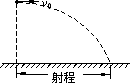
(1)若在此空间加上一个竖直方向的匀强电场使小球的射程增加为原来的1/2倍,试求此电场的电场强度.
(2)若除存在上述电场外,还存在一个与v0方向垂直的水平方向匀强磁场,使小球抛出后恰好能做匀速直线运动.试求此匀强磁场的磁感应强度.
(3)若在空间存在上述的电场和磁场,而将带电小球的初速度大小变为2v0(方向不变),试说明小球运动过程中动能最小时的速度方向.
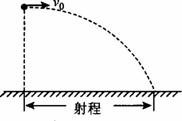
(1)若在此空间加上一个竖直方向的匀强电场使小球的射程增加为原来的2倍,试求此电场的电场强度;
(2)若除存在上述电场外,还存在一个与v0方向垂直的水平方向匀强磁场,使小球抛出后恰好能做匀速直线运动。试求此匀强磁场的磁感应强度;
(3)若在空间存在上述的电场和磁场,而将带电小球的初速度大小变为v0/2(方向不变),且小球并没有落至地面,试说明小球运动过程中动能最大时的速度方向。
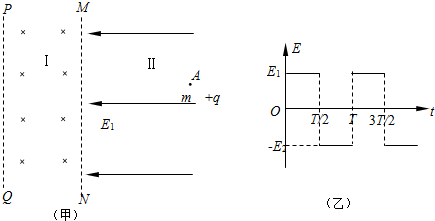
如图甲所示,空间Ⅰ区域存在方向垂直纸面向里的有界匀强磁场,左右边界线MN与PQ相互平行,MN右侧空间Ⅱ区域存在一周期性变化的匀强电场,方向沿纸面垂直MN边界,电场强度的变化规律如图乙所示(规定向左为电场的正方向).一质量为m、电荷量为+q的粒子,在t=0时刻从电场中A点由静止开始运动,粒子重力不计.
(1)若场强大小E1=E2=E,A点到MN的距离为L,为使粒子进入磁场时速度最大,交变电场变化周期的最小值T0应为多少?粒子的最大速度v0为多大?
(2)设磁场宽度为d,改变磁感应强度B的大小,使粒子以速度v1进入磁场后都能从磁场左边界PQ穿出,求磁感应强度B满足的条件及该粒子穿过磁场时间t的范围.
(3)若电场的场强大小E1=2E0,E2=E0,电场变化周期为T,t=0时刻从电场中A点释放的粒子经过n个周期正好到达MN边界,假定磁场足够宽,粒子经过磁场偏转后又回到电场中,向右运动的最大距离和A点到MN的距离相等.求粒子到达MN时的速度大小v和匀强磁场的磁感应强度大小B.
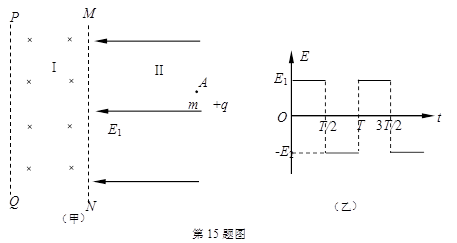
如图甲所示,空间Ⅰ区域存在方向垂直纸面向里的有界匀强磁场,左右边界线MN与PQ相互平行,MN右侧空间Ⅱ区域存在一周期性变化的匀强电场,方向沿纸面垂直MN边界,电场强度的变化规律如图乙所示(规定向左为电场的正方向).一质量为m、电荷量为+q的粒子,在t=0时刻从电场中A点由静止开始运动,粒子重力不计.
(1)若场强大小E1=E2=E,A点到MN的距离为L,为使粒子进入磁场时速度最大,交变电场变化周期的最小值T0应为多少?粒子的最大速度v0为多大?
(2)设磁场宽度为d,改变磁感应强度B的大小,使粒子以速度v1进入磁场后都能从磁场左边界PQ穿出,求磁感应强度B满足的条件及该粒子穿过磁场时间t的范围.
(3)若电场的场强大小E1=2E0,E2=E0,电场变化周期为T,t=0时刻从电场中A点释放的粒子经过n个周期正好到达MN边界,假定磁场足够宽,粒子经过磁场偏转后又回到电场中,向右运动的最大距离和A点到MN的距离相等.求粒子到达MN时的速度大小v和匀强磁场的磁感应强度大小B.
一单项选择题:本题共6小题,每小题3分,共18分
1. 1.D 2.A 3.C 4.B 5.D 6.A
二多项选择题:本题共5小题,每小题4分,共20分。全部选对的得4分,选对但不全的得2分,错选或不答的得0分
7.ABD 8.BC 9.ABC 10.AD 11.ACD
三实验题:本题共 2小题,共 23分
12.(1)1.880(1.881给分) (2分); 1.044 (2分)
(2)①
13.
 (1) 图 (3分) (2) 0-3V(2分) R1 (2分) (3) 图(4分)
(1) 图 (3分) (2) 0-3V(2分) R1 (2分) (3) 图(4分)

四 计算或论述题
14.地球绕太阳运动  3分
3分
太阳的质量
 3分
3分
(2)设小行星运行周期为T1  2分
2分
对小行星: 2分
2分
∴R1= 2分
2分
∴小行星与地球最近距离S=R1?R= 2分
2分
15.解:(1)由粒子的飞行轨迹,利用左手定则可知,该粒子带负电荷.粒子由A点射入,由C点飞出,其速度方向改变了90°,则粒子轨迹半径
 2分
2分
又  2分
2分
则粒子的比荷  2分
2分
(2)粒子从D点飞出磁场速度方向改变了60°角,故AD弧所对圆心角60°,粒子做圆周运动的半径

 2分
2分
又  2分
2分
所以  2分
2分
粒子在磁场中飞行时间
 2分
2分
16. (1)设共同加速度a,绳拉力F
有 mg-F=ma
F-μMg=Ma 3分
得到
 4分
4分
(2)当M运动h距离时速度为v,  1分
1分
又M运动s距离停止,由动能定理
 2分
2分
M物块不撞到定滑轮满足  1分
1分
得到 
代入得  2分
2分
因为要拉动M  结果是
结果是  2分
2分
17.(1) 要求当R=0时, E/R0≤I0
所以 R0≥E/ I0 3分
(2) 电量-q的粒子经过电压U加速后速度v0

 2分
2分
粒子进入Q场区域做半径r0,的匀速圆周运动
 2分
2分


 3分
3分
显然加速电压U 与与-q没有关系,所以只要满足上面关系,不同的负电荷都能绕Q做半径r0,的匀速圆周运动。
(3) 
即
 3分
3分
 2分
2分
18.(1)最大速度时拉力与安培力合力为零
P/v0-BIL=0 E=BL v。 I=E/(R+ R0)
即  3分
3分
 2分
2分
(2)由能量关系,产生总电热Q

 2分
2分
R电阻上所产生的电热
 2分
2分
(3) 
由(1)问可知 F=2P/v0 2分
当速度为v0时加速度a  2分
2分
解得

 2分
2分
19.(1)AB第一次与挡板碰后 A返回速度为v0
由动量守恒定律得 mA v0=(mA+mB) v1
∴v1=
(2)A相对于B滑行ΔS1
由动能定理得
μmAgΔS1= v02-
v02- (mA+mB) v12
(mA+mB) v12
ΔS1==
(3)AB与N碰撞后,返回速度大小为v2,则v2= v1
B与M相碰后停止,设A减速至零A相对B滑行ΔS1/
-μmAgΔS1/=0- v22 ΔS1/=
v22 ΔS1/=
∴A能与M碰撞第二次 3分
(4) A与M第一次碰撞速度为v1(v1= v0)
mA v1(mA+mB) v1/ ∴ v1/= v1
v1
A相对于B滑行ΔS1
μmAgΔS1= v12
v12 (mA+mB) v1/2
(mA+mB) v1/2
ΔS1= 2分
2分
当B再次与M相碰而静止时,A相对于B能滑行的最大距离为Sm1
0-v1/2=-2μg Sm1
Sm1= >ΔS1
>ΔS1
同理 每次以共同速度相碰,A都能相对B滑行到与M相碰,最终都停在M处 1分
A与M第二次碰撞速度为v2
则v22-v1/2=-2μgΔS1
v22= v12-2μgΔS1=
v12-2μgΔS1= ×6ΔS1-2ΔS1=
×6ΔS1-2ΔS1= ΔS1
ΔS1
同理ΔS2= =
= ΔS1
2分
ΔS1
2分
依次类推ΔS3== ΔS2
ΔS2
ΔS=(ΔS1+ΔS2+ΔS3+……) 2=
2= 2分
2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com