
题目列表(包括答案和解析)
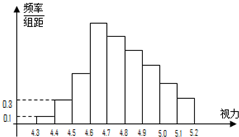 为了解某校高二学生的视力情况,随机地抽查了该校100名高二学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为B,视力在4.6到5.0之间的学生数为F.
为了解某校高二学生的视力情况,随机地抽查了该校100名高二学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为B,视力在4.6到5.0之间的学生数为F.(本小题满分13分)
我校要用三辆汽车把高二文科学生从学校送到古田参加社会实践活动,已知学校到古田有两条公路,汽车走公路①堵车的概率为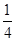 ,不堵车的概率为
,不堵车的概率为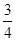 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为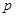 ,不堵车的概率为
,不堵车的概率为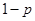 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
(I)若三辆汽车中恰有一辆汽车被堵的概率为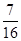 ,求汽车走公路②堵车的概率P。
,求汽车走公路②堵车的概率P。
(II)在(1)的条件下,求三辆汽车中被堵车辆的个数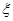 的分布列和数学期望。
的分布列和数学期望。
(本小题满分13分)
我校要用三辆汽车把高二文科学生从学校送到古田参加社会实践活动,已知学校到古田有两条公路,汽车走公路①堵车的概率为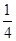 ,不堵车的概率为
,不堵车的概率为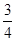 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为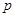 ,不堵车的概率为
,不堵车的概率为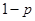 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
(I)若三辆汽车中恰有一辆汽车被堵的概率为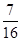 ,求汽
,求汽 车走公路②堵车的概率P。
车走公路②堵车的概率P。
(II)在(1)的条件下,求三辆汽车中被堵车辆的个数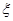 的分布列和数学期望。
的分布列和数学期望。
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.由于计算机操作员误将一些数据删去,请你先分析下面不完整的频率分布表,再结合算法流程图可知最后的输出结果S等于( )

| 序号(i) | 分组(分数) | 组中值(Gi) | 频数(人数) | 频率(Fi) |
| 1 | [60,70) | 65 | ① | 0.16 |
| 2 | [70,80) | 75 | 22 | ② |
| 3 | [80,90) | 85 | 14 | 0.28 |
| 4 | [90,100] | 95 | ③ | ④ |
| 合计 | 50 | 1 | ||
A.78.6 B.87.6
C.67.2 D.76.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com