（本题满分8分）在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图所示），已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12，请解答下列问题：

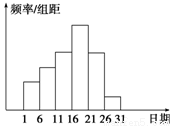
（1）本次活动共有多少件作品参加评比？

（2）哪组上交的作品数量最多？有多少件？

（3）经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率高？

（本题满分18分，第（1）小题6分，第（2）小题6分，第（3）小题6分）

若数列满足：是常数），则称数列为二阶线性递推数列，且定义方程为数列的特征方程，方程的根称为特征根； 数列的通项公式均可用特征根求得：

①若方程有两相异实根，则数列通项可以写成，（其中是待定常数）；

②若方程有两相同实根，则数列通项可以写成，（其中是待定常数）；

再利用可求得，进而求得．

根据上述结论求下列问题：

（1）当，（）时，求数列的通项公式；

（2）当，（）时，求数列的通项公式；

（3）当，（）时，记，若能被数整除，求所有满足条件的正整数的取值集合．

(本题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

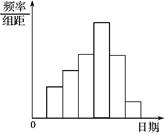
(1)本次活动共有多少件作品参加评比?

(2)哪组上交的作品数量最多?有多少件?

(3)经过评比,第四组和第六组分别有10件?2件作品获奖,问这两组哪一组获奖率较高?

（本小题满分12分）在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图所示），已知从左到右各长方形的高的比为2:3:4:6:4:1，第三组的频数为12，请解答下列问题：

    （1）本次活动共有多少件作品参加评比？

    （2）哪组上交的作品数量多？有多少件？

    （3）经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率较高？

（本题满分8分）在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图所示），已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12，请解答下列问题：

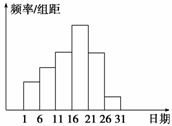
（1）本次活动共有多少件作品参加评比？

（2）哪组上交的作品数量最多？有多少件？

（3）经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率高？