
题目列表(包括答案和解析)
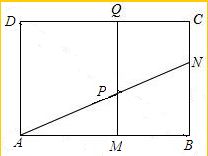 如图,在矩形ABCD中,AD=3厘米,AB=a厘米(a>3),动点M,N同时从B点出发,分别沿BA,BC方向运动,速度都是1厘米/秒,过M作直线垂直于AB,分别交AN,CD于P,Q,当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.
如图,在矩形ABCD中,AD=3厘米,AB=a厘米(a>3),动点M,N同时从B点出发,分别沿BA,BC方向运动,速度都是1厘米/秒,过M作直线垂直于AB,分别交AN,CD于P,Q,当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.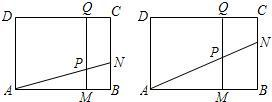 N的面积都相等?若存在,求a的值;若不存在,请说明理由.
N的面积都相等?若存在,求a的值;若不存在,请说明理由.如图,矩形 中,
中,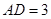 厘米,
厘米, 厘米(
厘米( ).动点
).动点 同时从
同时从 点出发,分别沿
点出发,分别沿 ,
, 运动,速度是
运动,速度是 厘米/秒.过
厘米/秒.过 作直线垂直于
作直线垂直于 ,分别交
,分别交 ,
, 于
于 .当点
.当点 到达终点
到达终点 时,点
时,点 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为 秒.
秒.
(1)若 厘米,
厘米, 秒,则
秒,则 ______厘米;
______厘米;
(2)若 厘米,求时间
厘米,求时间 ,使
,使 ,并求出它们的相似比;
,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形 与梯形
与梯形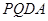 的面积相等,求
的面积相等,求 的取值范围;
的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形 ,梯形
,梯形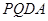 ,梯形
,梯形 的面积都相等?若存在,求
的面积都相等?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本题11分)如图所示,矩形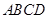 中,
中, 厘米,
厘米,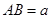 厘米(
厘米( ).动点
).动点 同时从
同时从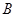 点出发,分别沿
点出发,分别沿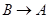 ,
,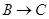 运动,速度是
运动,速度是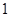 厘米/秒.过
厘米/秒.过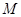 作直线垂直于
作直线垂直于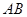 ,分别交
,分别交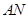 ,
,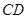 于
于 .当点
.当点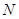 到达终点
到达终点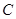 时,点
时,点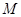 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为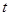 秒.
秒.
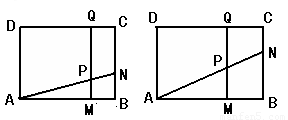
(1)若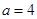 厘米,
厘米,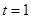 秒,求PM的长度;
秒,求PM的长度;
(2)若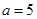 厘米,求出某个时间
厘米,求出某个时间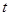 ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求 的取值范围;
的取值范围;
(本题11分)如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
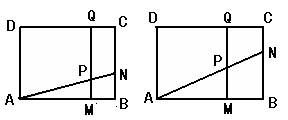
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
一、填空题:
1.60°.
2.答案不惟一,如:AE=CF,∠AEB=∠CFD,∠ ABE=∠CDF;
3.1;
4.4。
5.60
.files/image745.jpg)
7.2.files/image747.gif) -2
-2
8.15。
9.5
10.4
11.5
12. 2,3,n。
.files/image749.jpg)
14..files/image751.gif)
15. (-8,0)。
16.6。
17. .平行四边形。
18.60
19.4,12
二、选择题:
1.C
2.C
3.B
4.B
5.B
6.A
7.C。
8.B。
9.C
10.D
11.C。
12.B
13.B
14.C
15.D
16. C
17.C
18.D
19.D
20.C
21.D
22.D。
三、解答题:
1.(1)如图答2,因为AD∥BC,AB∥DC ------------------------------------------------- 2分
所以四边形ABCD为平行四边形.---------------------------------------------------------------- 3分
分别过点B、D作BF⊥AD,DE⊥AB,垂足分别为点E、F.
则BE = CF.-------------------------------------------------------------------------------------------- 4分
因为∠DAB =∠BAF,所以Rt△DAB≌Rt△BAF.--------------------------------------------- 5分
所以AD = AB.
所以四边形ABCD为菱形.-------------------------------------------------------------------------- 6分
(2)存在最小值和最大值.-------------------------------------------------------------------------- 7分
① 当∠DAB = 90°时,菱形ABCD为正方形,周长最小值为8;---------------------------8分
② 当AC为矩形纸片的对角线时,设AB = x,如图答3,在Rt△BCG中,
.files/image754.gif)
.files/image756.gif) ,
,.files/image758.gif) .所以周长最大值为17.-------------------------------------------9分
.所以周长最大值为17.-------------------------------------------9分
2.证明: ∵EF垂直平分AC,∴EF⊥AC,且AO=CO-------------------------------1′
证得:△AOE≌△COF-----------------------------------------------------------3′
证得:四边形AECF是平行四边形------------------------------------------------5′
由AC⊥EF可知:四边形AECF是菱形 -------------------------------------------6′
.files/image760.jpg)
.files/image762.jpg)
5.(本题满分8分)
解:(1)方法一:如图①
∵在□ ABCD中,AD∥BC
∴∠DAB+∠ABC=180° ………………………1分
∵AE、BF分别平分∠DAB和∠ABC
∴∠DAB=2∠BAE,∠ABC=2∠ABF ………………………2分
∴2∠BAE+2∠ABF=180°
即∠BAE+∠ABF=90° ………………………3分
∴∠AMB=90°
.files/image764.gif) ∴AE⊥BF.
…………………………4分
∴AE⊥BF.
…………………………4分
.files/image765.gif) |
|||
|