
题目列表(包括答案和解析)
如图甲,在 中,
中,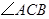 为锐角,点
为锐角,点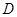 为射线
为射线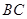 上一点,连接
上一点,连接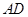 ,以
,以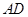 为一边且在
为一边且在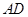 的右侧作正方形
的右侧作正方形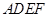 .解答下列问题:
.解答下列问题: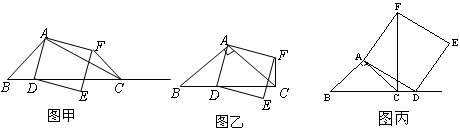
(1)如果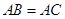 ,
,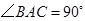 ,
,
①当点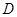 在线段
在线段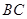 上时(与点
上时(与点 不重合),如图乙,线段
不重合),如图乙,线段 之间的位置关系为 ,数量关系为 .
之间的位置关系为 ,数量关系为 .
②当点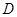 在线段
在线段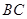 的延长线时,如图丙,①中的结论是否仍然成立,为什么?
的延长线时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果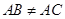 ,
,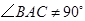 ,点
,点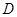 在线段
在线段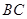 上运动.试探究:当
上运动.试探究:当 满足一个什么条件时,
满足一个什么条件时,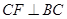 (点
(点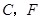 重合除外)?画出图形,并说明理由.(画图不写作法).
重合除外)?画出图形,并说明理由.(画图不写作法).
如图甲,在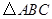 中,
中,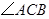 为锐角,点
为锐角,点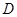 为射线
为射线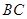 上一点,连接
上一点,连接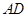 ,以
,以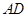 为一边且在
为一边且在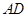 的右侧作正方形
的右侧作正方形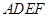 .解答下列问题:
.解答下列问题:
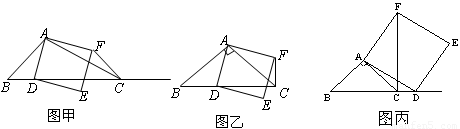
(1)如果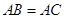 ,
,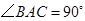 ,
,
①当点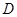 在线段
在线段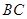 上时(与点
上时(与点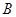 不重合),如图乙,线段
不重合),如图乙,线段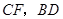 之间的位置关系为 ,数量关系为 .
之间的位置关系为 ,数量关系为 .
②当点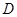 在线段
在线段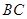 的延长线时,如图丙,①中的结论是否仍然成立,为什么?
的延长线时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果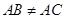 ,
,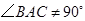 ,点
,点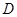 在线段
在线段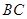 上运动.试探究:当
上运动.试探究:当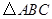 满足一个什么条件时,
满足一个什么条件时,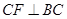 (点
(点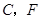 重合除外)?画出图形,并说明理由.(画图不写作法).
重合除外)?画出图形,并说明理由.(画图不写作法).
已知:正方形 的边长为1,射线
的边长为1,射线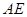 与射线
与射线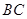 交于点
交于点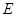 ,射线
,射线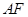 与射线
与射线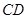 交于点
交于点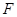 ,
,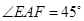 .
.
(1)如图1,当点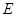 在线段
在线段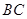 上时,试猜想线段
上时,试猜想线段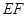 、
、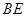 、
、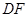 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想.
(2)设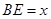 ,
,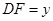 ,当点
,当点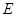 在线段
在线段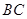 上运动时(不包括点
上运动时(不包括点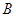 、
、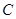 ),如图1,求
),如图1,求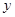 关于
关于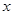 的函数解析式,并指出
的函数解析式,并指出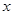 的取值范围.
的取值范围.
(3)当点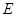 在射线
在射线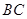 上运动时(不含端点
上运动时(不含端点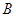 ),点
),点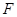 在射线
在射线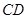 上运动.试判断以
上运动.试判断以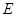 为圆心以
为圆心以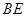 为半径的
为半径的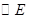 和以
和以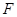 为圆心以
为圆心以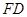 为半径的
为半径的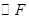 之间的位置关系.
之间的位置关系.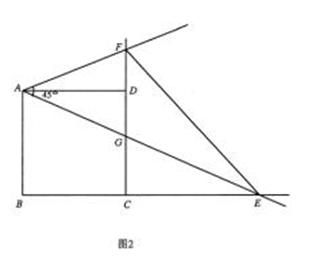
(4)当点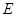 在
在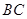 延长线上时,设
延长线上时,设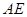 与
与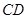 交于点
交于点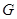 ,如图2.问△
,如图2.问△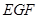 与△
与△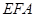 能否相似,若能相似,求出
能否相似,若能相似,求出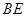 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.
(本小题满分9分)
在 中,
中, ,点
,点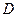 在
在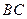 所在的直线上运动,作
所在的直线上运动,作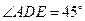 (
(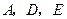 按逆时针方向).
按逆时针方向).
(1)如图1,若点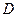 在线段
在线段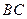 上运动,
上运动,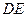 交
交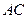 于
于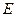 .
.
①问△ABD与△DCE相似吗?为什么?
②当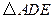 是等腰三角形时,求
是等腰三角形时,求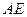 的长.
的长.
(2)① 如图2,若点
如图2,若点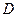 在
在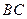 的延长线上运动,
的延长线上运动,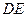 的反向延长线与
的反向延长线与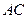 的延长线相交于点
的延长线相交于点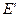 ,是否存在点
,是否存在点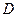 ,使
,使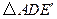 是等腰三角形?若存在,写出所有点
是等腰三角形?若存在,写出所有点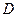 的位置;若不存在,请简要说明理由;
的位置;若不存在,请简要说明理由;
②如图3,若点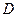 在
在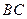 的反向延长线上运动,是否存在点
的反向延长线上运动,是否存在点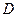 ,使
,使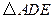 是等腰三角形?若存在,写出所有点
是等腰三角形?若存在,写出所有点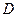 的位置;若不存在,请简要说明理由.
的位置;若不存在,请简要说明理由.
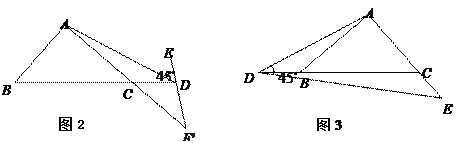
如图1,梯形 中,
中, ∥
∥ ,
,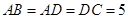 ,
, .一个动点
.一个动点 从点
从点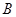 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点 在射线
在射线 上,当
上,当 点到达
点到达 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒( ).
).
(1)当正方形 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设正方形 与△
与△ 的重合部分面积为
的重合部分面积为 ,请直接写
,请直接写
出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图2,当点 在线段
在线段 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△
沿 翻折,得到△
翻折,得到△ ,连接
,连接 .是否存在这样的
.是否存在这样的 ,使△
,使△ 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.


一、填空题:
1.60°.
2.答案不惟一,如:AE=CF,∠AEB=∠CFD,∠ ABE=∠CDF;
3.1;
4.4。
5.60
.files/image745.jpg)
7.2.files/image747.gif) -2
-2
8.15。
9.5
10.4
11.5
12. 2,3,n。
.files/image749.jpg)
14..files/image751.gif)
15. (-8,0)。
16.6。
17. .平行四边形。
18.60
19.4,12
二、选择题:
1.C
2.C
3.B
4.B
5.B
6.A
7.C。
8.B。
9.C
10.D
11.C。
12.B
13.B
14.C
15.D
16. C
17.C
18.D
19.D
20.C
21.D
22.D。
三、解答题:
1.(1)如图答2,因为AD∥BC,AB∥DC ------------------------------------------------- 2分
所以四边形ABCD为平行四边形.---------------------------------------------------------------- 3分
分别过点B、D作BF⊥AD,DE⊥AB,垂足分别为点E、F.
则BE = CF.-------------------------------------------------------------------------------------------- 4分
因为∠DAB =∠BAF,所以Rt△DAB≌Rt△BAF.--------------------------------------------- 5分
所以AD = AB.
所以四边形ABCD为菱形.-------------------------------------------------------------------------- 6分
(2)存在最小值和最大值.-------------------------------------------------------------------------- 7分
① 当∠DAB = 90°时,菱形ABCD为正方形,周长最小值为8;---------------------------8分
② 当AC为矩形纸片的对角线时,设AB = x,如图答3,在Rt△BCG中,
.files/image754.gif)
.files/image756.gif) ,
,.files/image758.gif) .所以周长最大值为17.-------------------------------------------9分
.所以周长最大值为17.-------------------------------------------9分
2.证明: ∵EF垂直平分AC,∴EF⊥AC,且AO=CO-------------------------------1′
证得:△AOE≌△COF-----------------------------------------------------------3′
证得:四边形AECF是平行四边形------------------------------------------------5′
由AC⊥EF可知:四边形AECF是菱形 -------------------------------------------6′
.files/image760.jpg)
.files/image762.jpg)
5.(本题满分8分)
解:(1)方法一:如图①
∵在□ ABCD中,AD∥BC
∴∠DAB+∠ABC=180° ………………………1分
∵AE、BF分别平分∠DAB和∠ABC
∴∠DAB=2∠BAE,∠ABC=2∠ABF ………………………2分
∴2∠BAE+2∠ABF=180°
即∠BAE+∠ABF=90° ………………………3分
∴∠AMB=90°
.files/image764.gif) ∴AE⊥BF.
…………………………4分
∴AE⊥BF.
…………………………4分
.files/image765.gif) |
|||
|