
题目列表(包括答案和解析)
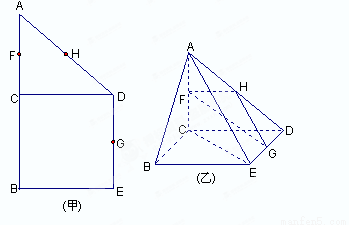
(本小题满分13分)如图(甲),在直角梯形ABED中,AB//DE,AB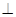 BE,AB
BE,AB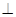 CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD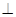 平面CBED,如图(乙).
平面CBED,如图(乙).
(1)求证:平面FHG//平面ABE;
(2)记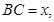
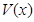 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求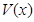 的最大值;
的最大值;
(3)当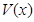 取得最大值时,求二面角D-AB-C的余弦值.
取得最大值时,求二面角D-AB-C的余弦值.
(本小题满分14分)已知梯形ABCD中,AD∥BC,∠ABC
=∠BAD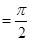 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE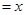 ,G是BC的中点.沿EF将梯形ABCD翻折,
,G是BC的中点.沿EF将梯形ABCD翻折,
使平面AEFD⊥平面EBCF (如图).
(1)当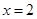 时,求证:BD⊥EG ;
时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(3)当 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
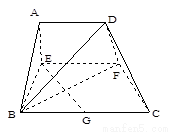

在![]() 中,
中,![]() ,当
,当![]() 取得最大值时三角形的形状是 ( )
取得最大值时三角形的形状是 ( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
已知向量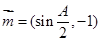 ,
,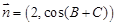 ,
,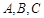 为锐角
为锐角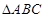 的内角,
的内角,
其对应边为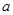 ,
, ,
,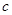 .
.
(Ⅰ)当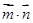 取得最大值时,求角
取得最大值时,求角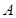 的大小;
的大小;
(Ⅱ)在(Ⅰ)成立的条件下,当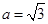 时,求
时,求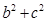 的取值范围.
的取值范围.
设正实数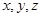 满足
满足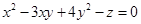 ,则当
,则当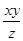 取得最大值时,
取得最大值时,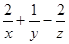 的最大值为(
)
的最大值为(
)
A. B.
B. C.
C.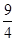 D.
D.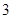
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com