
题目列表(包括答案和解析)
y 社区数量 x |
居民素质 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
| 社 区 服 务 |
1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | a | b | 6 | 0 | 1 | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
| 167 |
| 50 |
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
(本题满分12分)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
| A | B | C | D | E | |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) |
⑴在上表中填写出各人应缴的话费;
⑵设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | ||||
| 4<t≤5 | ||||
| 5<t≤6 | ||||
| 合计 | 正 正 |
⑶若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算)。问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
|
|
A |
B |
C |
D |
E |
|
第一次通话时间 |
3分 |
3分45秒 |
3分55秒 |
3分20秒 |
6分 |
|
第二次通话时间 |
0分 |
4分 |
3分40秒 |
4分50秒 |
0分 |
|
第三次通话时间 |
0分 |
0分 |
5分 |
2分 |
0分 |
|
应缴话费(元) |
|
|
|
|
|
(1)在上表中填写出各人应缴的话费;
(2)设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
|
时间段 |
频数累计 |
频数 |
频率 |
累计频率 |
|
0<t≤3 |
┯ |
2 |
0.2 |
0.2 |
|
3<t≤4 |
|
|
|
|
|
4<t≤5 |
|
|
|
|
|
5<t≤6 |
|
|
|
|
|
合计 |
正 正 |
|
|
|
(3)若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算)。问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本试题主要考查了线面平行的判定定理和线面垂直的判定定理,以及二面角的求解的运用。中利用 ,又
,又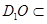 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得证明
.
可得证明
(3)因为∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴利用法向量的夹角公式,
的法向量.∴利用法向量的夹角公式, ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为 .
.
方法一:解:(Ⅰ)建立如图所示的空间直角坐标系.连接 ,则点
,则点 、
、 ,
,

∴ ,又点
,又点 ,
, ,∴
,∴
∴ ,且
,且 与
与 不共线,∴
不共线,∴ .
.
又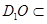 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴
的法向量.∴ ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com