题目列表(包括答案和解析)
（08年天津南开区质检二文） （12分）
已知等比数列
，公比q，Sn的前n项的和，且
。
（1）求数列的通项公式；
（2）设
，求数列
的前
项和
；
（3）比较（2）中与
的大小，并说明理由。
（08年天津南开区质检二文） （12分）
已知等比数列
，公比q，Sn的前n项的和，且
。
（1）求数列的通项公式；
（2）设
，求数列
的前
项和
；
（3）比较（2）中与
的大小，并说明理由。
（本小题满分14分）
设
（
且
），g(x)是f(x)的反函数.
（Ⅰ）求
；
（Ⅱ）当
时，恒有
成立，求t的取值范围；
（Ⅲ）当0＜a≤时，试比较f(1)+f(2)+…+f(n)与
的大小，并说明理由.
（Ⅰ）求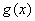
；
（Ⅱ）当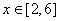
时，恒有
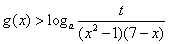成立，求t的取值范围；
（Ⅲ）当0＜a≤时，试比较f(1)+f(2)+…+f(n)与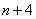
的大小，并说明理由.
（本小题满分14分）
设
（
且
），g(x)是f(x)的反函数.
（Ⅰ）求
；
（Ⅱ）当
时，恒有
成立，求t的取值范围；
（Ⅲ）当0＜a≤时，试比较f(1)+f(2)+…+f(n)与
的大小，并说明理由.
一、选择题（60分）
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
C
B
（C
D
D
A
B
C
B
二、填空题（20分）
13. 15 14．5 15． 
16． 
三、解答题（70分）
17．（1）
，∴
，∴
（5分）
（2）
∵
，∴
，∴
∴
（理10分）
18．
（1）记“甲恰好投进两球”为事件A，则
（6分）
（2）记“甲比乙多投进两球”，其中“恰好甲投进两球且乙未投进”为事件
，“恰好甲投进三球且乙投进一球”为事件
，根据提议，、互斥，
（理12分）
19．（1） （6分）
（2） （文12分）
（3） （理12分）
20．（1）设数列
的公比为
，则
∴
则
（文6分，理4分）
（2）由（1）可知
所以数列
是一个以
为首项，1为公差的等差数列
∴
（文12分，理8分）
（3）∵
∴当
时，
，即
当
时，
，即
综上可知：时，；时， （理12分）
21. ⑴由已知
所求双曲线C的方程为
;
⑵设P点的坐标为
,M,N的纵坐标分别为
.
共线
同理
22．
（1）由题意得：
∴在
上
；在
上
；在
上
在此
在
处取得极小值
∴
①
②
③
由①②③联立得：
∴
（6分）
（2）设切点Q
过
令
，
求得：
，方程
有三个根。
需：
故：
因此所求实数
的取值范围为：
（理12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com