题目列表(包括答案和解析)
.(本题满分13分）设函数
，方程f(x)=x有唯一的解，
已知f(xn)=xn+1(n∈N﹡)且f(xl)=
．
(1)求证：数列{
）是等差数列；
(2)若
，求Sn=b1+b2+b3+…+bn
(3)在(2)的条件下，是否存在最小正整数m，使得对任意n∈N﹡，有
成立，若存在，求出m的值；若不存在，请说明理由。
设单调递增函数
的定义域为
，且对任意的正实数x,y有：
且
．
⑴．一个各项均为正数的数列
满足:
其中
为数列的前n项和,求数列的通项公式；
⑵．在⑴的条件下，是否存在正数M使下列不等式：
对一切
成立？若存在，求出M的取值范围；若不存在，请说明理由．
设单调递增函数
的定义域为
，且对任意的正实数x,y有：
且
．
⑴、一个各项均为正数的数列
满足:
其中
为数列的前n项和,求数列的通项公式；
⑵、在⑴的条件下，是否存在正数M使下列不等式：
对一切
成立？若存在，求出M的取值范围；若不存在，请说明理由．
已知函数f(x)=x3-ax2-3x
①若f(x)在区间[1，+∞）上是增函数，求实数a的取值范围；
②若x=-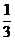
是f(x)的极值点，求f(x)在[1，a]上的最大值；
③在②的条件下，是否存在实数b，使得函数g(x)=bx的图象与f(x)的图象恰有3个交点，若存在，请求出实数b的取值范围；若不存在，试说明理由.
（08年丰台区统一练习一理）（13分）
在平面直角坐标系xOy中，已知点A(-1, 0)、B(1, 0), 动点C满足条件：△ABC的周长为
.记动点C的轨迹为曲线W.
(Ⅰ)求W的方程；
(Ⅱ)经过点（0, 
）且斜率为k的直线l与曲线W 有两个不同的交点P和Q，
求k的取值范围；
（Ⅲ）已知点M（
），N（0, 1），在(Ⅱ)的条件下，是否存在常数k，使得向量
与
共线？如果存在，求出k的值；如果不存在，请说明理由.
1．B 2 D． 3．B 4．C 5．C 6．C 7．B 8．C 9．D 10．B
11．D 12．B
13．240 14．1 15．
16.
①②③
17．（本题满分10分）
解：(Ⅰ)由
又
(Ⅱ)
同理：
故
，
，
.
18．（本题满分12分）
解：(Ⅰ)记“这批太空种子中的某一粒种子既发芽又发生基因突变”为事件
，则
.
(Ⅱ) 
19．（本题满分12分）
解
(Ⅰ)∵
，∴{
}是公差为4的等差数列，
∵a1=1, =
+4(n－1)=4n－3,∵an>0,∴an=
(Ⅱ)bn=Sn+1－Sn=an+12=
,由bn<
,得m>
,
设g(n)= ,∵g(n)= 在n∈N*上是减函数，
∴g(n)的最大值是g(1)=5,
∴m>5,存在最小正整数m=6,使对任意n∈N*有bn<成立
20．（本题满分12分）
解法一：
（I）设
是
的中点，连结
，则四边形
为正方形，
．故
，
，
，
，即
．
又
，
平面
，
（II）由（I）知
平面，
又
平面，
，
取
的中点
, 连结
，又
，则
．
取
的中点
，连结
，则
,
.
为二面角
的平面角．
连结
，在
中，
，
，
取
的中点
，连结
，
，
在
中，
，
，
．
．
二面角的余弦值为
．
解法二：
（I）以
为原点，
所在直线分别为
轴，
轴，
轴建立如图所示的空间直角坐标系，则
，
，
，
，
,
.
，
,
又因为 所以，平面
.
（II）设
为平面
的一个法向量．
由
，
，
得
取
，则
．
又
，，设
为平面
的一个法向量，
由
，
，得
取
，则
，
设
与
的夹角为
，二面角为
，显然为锐角，
,
21．（本题满分12分）
解：(Ⅰ) 
,
在
上是增函数，在
上是减函数,
∴当
时, 取得极大值.
∴
即
.
由
,
得
,
则有 
,
递增
极大值4
递减
极小值0
递增
所以, 当
时,函数的极大值为4;极小值为0; 单调递增区间为和.
(Ⅱ) 由(Ⅰ)知, 
,
的两个根分别为
. ∵在上是减函数,∴
,即
,
.
22．（本题满分12分）
解:（I）依题意，可知
，
∴ 
，解得
∴椭圆的方程为
（II）直线
：
与⊙
相切，则
，即
，
由
，得
，
∵直线与椭圆交于不同的两点
设
∴
，
，
∴
∴
∴
，
∴
设
，则
，
∵
在
上单调递增
∴
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com