
题目列表(包括答案和解析)
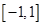 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围; 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为(本小题满分12分)已知:![]() ,
,![]() 为实常数.
为实常数.
(1) 求![]() 的最小正周期;
的最小正周期;
(2)![]() 在
在![]() 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求![]() 的值.
的值.
(本小题满分12分)
已知函数![]()
(1)若方程![]() 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)![]() 如果函数
如果函数![]() 的图象与x轴交于两点
的图象与x轴交于两点![]() 、
、![]() 且
且![]() .求证:
.求证:![]() (其中正常数
(其中正常数![]() ).
).
(本小题满分12分)
已知函数f(x)=alnx+x2(a为实常数).
(Ⅰ)若a=-2,求证:函数f(x)在(1,+∞)上是增函数;
(Ⅱ)求函数f(x)在[1,e]上的最小值及相应的x值;
(本小题满分12分)
已知椭圆C: (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右
顶点,定点A的坐标为(2,0).
(1)若M与A重合,求曲线C的焦点坐标.
(2)若 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.
(3)若|PA|最小值为|MA|,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com