
题目列表(包括答案和解析)
| 5 |
| 5 |
| OS |
| OA |
| OB |
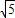 )2+y2=36,定点N(
)2+y2=36,定点N(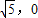 ),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|
),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|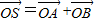 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 2 |
| n |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com