练习册

  • 练习册
  • 试题
    解:(1)设直线AB: 【查看更多】

     

    题目列表(包括答案和解析)

    解答题：解答应写出文字说明，证明过程或推演步骤

    如图，在平直河岸l的同一侧有两个缺水的居民区A、B，已知A、B到河岸的距离AD＝1千米，BC＝2千米，A、B之间的距离AB＝2千米．欲在河岸l上建一个抽水站，使得两居民区都能解决供水问题．

    (1)

    在河岸l上选取一点P建一个抽水站，从P分别铺设水管至居民区A、B，问点P应在什么位置，铺设水管的总长度最小？并求这个最小值；

    (2)

    从实际施的结果来看，工作人员将水管铺设至居民区A、B，且所铺设的水管总长度比(Ⅰ)中的最小值更小，你知道工作人员如何铺设水管吗(指出铺设线路，不必证明)？并算出实际铺设水管的总长度．

    查看答案和解析>>

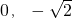    设椭圆C：数学公式（a＞b＞0）的一个顶点坐标为A（数学公式），且其右焦点到直线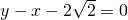数学公式的距离为3．
    （1）求椭圆C的轨迹方程；
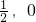    （2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M（数学公式），求证点M的所有“相关弦”的中点在同一条直线上；
    （3）根据解决问题（2）的经验与体会，请运用类比、推广等思想方法，提出一个与“相关弦”有关的具有研究价值的结论，并加以解决．（本小题将根据所提出问题的层次性给予不同的分值）

    查看答案和解析>>

    素材1：设抛物线y2=2px(p＞0)的焦点为F,AB过焦点F且不垂直于x轴;

    素材2：线段AB的垂直平分线l交x轴于N点.

    试根据上述素材构建一个问题，然后再解答.

    查看答案和解析>>

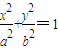    设椭圆C：（a＞b＞0）的一个顶点坐标为A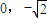（），且其右焦点到直线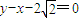的距离为3．
    （1）求椭圆C的轨迹方程；
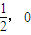    （2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M（），求证点M的所有“相关弦”的中点在同一条直线上；
    （3）根据解决问题（2）的经验与体会，请运用类比、推广等思想方法，提出一个与“相关弦”有关的具有研究价值的结论，并加以解决．（本小题将根据所提出问题的层次性给予不同的分值）

    查看答案和解析>>

     （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）

    A．（不等式选做题）若关于的不等式存在实数解，则实数的取值范围是             ．

    B．（几何证明选做题）如图，∠B=∠D，，，且AB=6，AC=4，AD=12，则BE=         ．

    C．（坐标系与参数方程选做题）直角坐标系中，以原点O为极点，轴的正半轴为极轴建立极坐标系，设点A，B分别在曲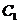线：（为参数）和曲线：上，则的最小值为                 ．

     

    查看答案和解析>>


    同步练习册答案