练习册

  • 练习册
  • 试题
    已知椭圆中心在原点.焦点在y轴上.焦距为4.离心率为 (Ⅰ)求椭圆方程, 【查看更多】

     

    题目列表(包括答案和解析)

    已知椭圆中心在原点，焦点在y轴上，离心率为
    		3
    3
    ，以原点为圆心，椭圆短半轴长为半径的圆与直线y=x+2相切．
    （Ⅰ）求椭圆的标准方程；
    （Ⅱ）设点F是椭圆在y轴正半轴上的一个焦点，点A，B是抛物线x2=4y上的两个动点，且满足
    AF
    =λ
    FB
     (λ＞0)    ，过点A，B分别作抛物线的两条切线，设两切线的交点为M，试推断
    FM
    •
    AB
    是否为定值？若是，求出这个定值；若不是，说明理由．

    查看答案和解析>>

    已知椭圆中心在原点，焦点在y轴上，离心率为，以原点为圆心，椭圆短半轴长为半径的圆与直线相切.

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设点F是椭圆在y轴正半轴上的一个焦点，点A，B是抛物线上的两个动点，且满足，过点A，B分别作抛物线的两条切线，设两切线的交点为M，试推断是否为定值？若是，求出这个定值；若不是，说明理由.

    查看答案和解析>>

    已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为．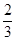

    （1）求椭圆方程；

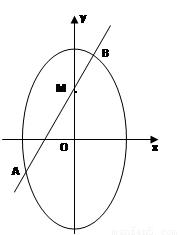
    （2）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段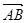所成的比为2，求线段AB所在直线的方程．

     

    查看答案和解析>>

    已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为．

    （I）求椭圆方程；

    （II）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段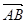所成的比为2，求线段AB所在直线的方程．

     

    查看答案和解析>>

    已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为．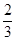

    （1）求椭圆方程；
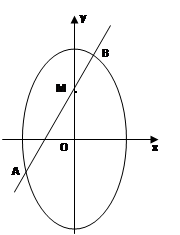
    （2）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段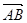所成的比为2，求线段AB所在直线的方程．

    查看答案和解析>>

     

    一、选择题

    A卷：BACDB    DCABD    BA

    B卷：BDACD    BDCAB    BA

    二、填空题

    13．15  

    14．210

    15．

    16．①④

    三、解答题：

    17． 解：（注：考试中计算此题可以使用分数，以下的解答用的是小数）

       （Ⅰ）同文（Ⅰ）

       （Ⅱ）的概率分别为

    随机变量的概率分布为

    0

    1

    2

    3

    P

    0.216

    0.432

    0.288

    0.064

    ………………8分

    的数学期望为E=0×0.216+1×0.432+2×0.288+3×0.064=1.2.…………10分

    （或利用E=mp=3×0.4=1.2）

    的方差为

    D=（0－1.2）2×0.216+（1－1.2）2×0.432+（2－1.2）2×0.288+（3－1.2）2×0.064

    =0.72.…………………………12分

    （或利用D=nq=3×0.4×0.6=0.72）

     

    18．解：

       （Ⅰ）

    …………4分

    所以，的最小正周期，最小值为－2.…………………………6分

       （Ⅱ）列表：

    x

    0

    2

    0

    －2

    0

     

     

     

     

     

     

     

     

     

     

     

     

    …………………12分

    （19?文）同18?理.

    （19?理）解：（Ⅰ）取A1A的中点P，连PM、PN，则PN//AD，

    …………………………6分

     

     

     

     

     

     

     

     

     

     

     

     

       （Ⅱ）由（Ⅰ）知，则就是所求二面角的平面角.………………………8分

             显然

    利用等面积法求得A1O=AO=在△A1OA中由余弦定理得

    cos∠A1OA=.

    所以二面角的大小为arccos……………………………………………12分

    （20?文）同19理.

    （20?理）（I）证明：当q>0时，由a1>0，知an>0，所以Sn>0；………………2分

    当－1<q<0时，因为a1>0，1－q>0，1－qn>0，所以.

    综上，当q>－1且q≠0时，Sn>0总成立.……………………5分

       （II）解：an+1=anq，an+2=anq2，所以bn=an+1－kan+2=an(q－kq2).

            Tn=b1+b2+…+bn=(a1+a2+…+an)(q－kq2)=Sn(q－kq2).……………………9分

            依题意，由Tn>kSn，得Sn(q－kq2)>kSn.

            ∵Sn>0，∴可得q－kq2>k，

    即k(1+q2)<q，k<.

    ∵

    ∴k的取值范围是. ……………………12分

    （21?文）解：f′(x)=3x2+4ax－b.………………………………2分

             设f′(x)=0的二根为x1，x2，由已知得

             x1=－1，x2≥2，………………………………………………4分

             …………………………7分

            解得

            故a的取值范围是…………………………………………12分

    （21?理）解：（I）设椭圆方程

            由2c=4得c=2，又.

            故a=3，b2=a2－c2=5，

            ∴所求的椭圆方程.…………………………………………5分

       （II）点F的坐标为（0，2），设直线AB的方程为y=kx+2,A(x1,y1)、B(x2，y2).

    由得(9+5k2)x2+20kx－25=0，………………………………8分

    显然△>0成立，

    根据韦达定理得

    ，                       ①

    .                           ②

    ,

    ,代入①、②得

                                         ③

                                        ④

    由③、④得

     …………………………………………14分

    （22．文）同21理，其中3分、6分、8分、12分依次更改为5分、8分、10分、14分.

    （22．理）（1）证明：令

    原不等式…………………………2分

    令，

    单调递增，，

    ………………………………………………5分

    令，

    单调递增，，

     …………………………………………8分

    ………………………………9分

       （Ⅱ）令，上式也成立

    将各式相加

    ……………11分

    即

    ……………………………………………………………………14分

     


    同步练习册答案