
题目列表(包括答案和解析)
(本小题满分12分)
甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件的二倍。
(1)从甲、乙、丙加工的零件中各取一件检验,示至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混![]() 合到一起,从中任意的抽取4件检验,其中一等品的个数记为X,求EX。
合到一起,从中任意的抽取4件检验,其中一等品的个数记为X,求EX。
(本小题满分12分)
甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件的二倍。
(1)从甲、乙、丙加工的零件中各取一件检验,示至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,其中一等品的个数记为X,求EX。
(本小题满分12分)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为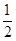 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(1)打了两局就停止比赛的概率;
(2)打满3局比赛还未停止的概率;
(3)比赛停止时已打局数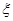 的分布列与期望
的分布列与期望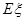 .
.
(本小题满分12分)
甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场。每场比赛胜者得3分,负者得0分,没有平局。在每一场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() 。
。
(1)求甲获第一名且丙获第二名的概率;
(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望。
(本小题满分12分)
甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场。每场比赛胜者得3分,负者得0分,没有平局。在每一场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() 。
。
(1)求甲获第一名且丙获第二名的概率;
(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望。
一、选择题
A卷:BACDB DCABD BA
B卷:BDACD BDCAB BA
二、填空题
13.15
14.210
15.
16.①④
三、解答题:
17.文 解:
(Ⅰ)3人各自进行1次实验都没有成功的概率
 …………………………6分
…………………………6分
(Ⅱ)甲独立进行3次实验至少有两次成功的概率
 …………………………12分
…………………………12分
17.理 解:(注:考试中计算此题可以使用分数,以下的解答用的是小数)
(Ⅰ)同文(Ⅰ)
(Ⅱ) 的概率分别为
的概率分别为




随机变量 的概率分布为
的概率分布为

0
1
2
3
P
0.216
0.432
0.288
0.064
………………8分
 的数学期望为E
的数学期望为E =0×0.216+1×0.432+2×0.288+3×0.064=1.2.…………10分
=0×0.216+1×0.432+2×0.288+3×0.064=1.2.…………10分
(或利用E =np=3×0.4=1.2)
=np=3×0.4=1.2)
 的方差为
的方差为
D =(0-1.2)2×0.216+(1-1.2)2×0.432+(2-1.2)2×0.288+(3-1.2)2×0.064
=(0-1.2)2×0.216+(1-1.2)2×0.432+(2-1.2)2×0.288+(3-1.2)2×0.064
=0.72.…………………………12分
(或利用D =npq=3×0.4×0.6=0.72)
=npq=3×0.4×0.6=0.72)
18.文 解:
(Ⅰ)设数列
所以 ……………………3分
……………………3分
所以 …………………………6分
…………………………6分
(Ⅱ) ………………9分
………………9分

………………12分
18.理 解:
(Ⅰ)
…………4分
所以, 的最小正周期
的最小正周期 ,最小值为-2.…………………………6分
,最小值为-2.…………………………6分
(Ⅱ)列表:
x
0







2
0
-2
0

|