练习册

  • 练习册
  • 试题
    如图1.两个相对平行放置的平面镜1和2.相距为6cm.两镜之间有一个 点.在平面镜1中的像为点.在平面镜2中的像为点.在平面镜1中的像为点.如此反复若干次.构成数列 (1) 若点到平面镜1的距离是3cm.求数列的通项公式, (2) 若点到平面镜1的距离是2cm.求数列的通项公式, 图1 解:(1)∵点位于平面镜1和2的正中间. ∴点到近端的平面镜的距离是.∴点到远端平面镜的距离是. ∵点是点在远端平面镜中所成的像. ∴点到近端平面镜的距离也是. ∴.即. 又∵. ∴数列是以6为首项.6为公差的等差数列. ∴ (2)∵点到平面镜1的距离是2. ∴若.则点位于平面镜1的下方. ∴此时点到平面镜2的距离是 ∴此时点到平面镜2的距离也是 ∴此时点到点的距离是.即 ∴ (*) 又∵若.则点位于平面镜2的上方. ∴此时点到平面镜1的距离是. ∴此时点到平面镜1的距离是也. ∴此时点到点的距离是.即 ∴ (*) 由得: 又∵. ∴数列的奇数项是以4为首项.12为公差的等差数列,偶数项是以12为首项.12为公差的等差数列 ∴ (注:若点在平面镜1的下方.则称平面镜1为近端平面镜.称平面镜2为远端平面镜.反之亦然) 【查看更多】

     

    题目列表(包括答案和解析)

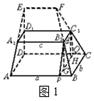
    如图1，在多面体ABCD—A1B1C1D1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E，F两点，上、下底面矩形的长、宽分别为c，d与a，b，且a＞c，b＞d，两底面间的距离为h。

    （Ⅰ）求侧面ABB1A1与底面ABCD所成二面角的大小；

    （Ⅱ）证明：EF∥面ABCD；

    （Ⅲ）在估测该多面体的体积时，经常运用近似公式V估=S中截面·h来计算.已知它的体积公式是V=（S上底面+4S中截面+S下底面），试判断V估与V的大小关系，并加以证明。

    （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面）

    查看答案和解析>>


    同步练习册答案