练习册

  • 练习册
  • 试题
    13．如图所示.质量M=4kg的滑板B静止放在光滑水平面上.其右端固定一根轻质弹簧.弹簧的自由端C到滑板左端的距离L = 0.5m.这段滑板与木块A之间的动摩擦因数＝0.2.而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑．可视为质点的小木块A以速度μ＝0.2.由滑板B左端开始沿滑板B表面向右运动．已知A的质量m = l kg.g 取10m/ s 2 .求: (1)弹簧被压缩到最短时木块A 的速度, (2)木块A 压缩弹簧过程中弹簧的最大弹性势能． 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，可视为质点的小木块A质量m=1kg，原来静止于滑板的左端，滑板与木块A之间的动摩擦因数μ=0.2．当滑板B受水平向左恒力F=14N作用时间t后，撤去F，这时木块A恰好到达弹簧自由端C处，此后运动过程中的最大压缩量为x=5cm．g取10m/s2，求：
    （1）水平恒力F的作用时间t
    （2）木块A压缩弹簧过程中弹簧的最大弹性势能；
    （3）整个运动过程中系统产生的热量．

    查看答案和解析>>

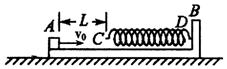    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，其右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，这段滑板与木块A之间的动摩擦因数μ＝0.2，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑．可视为质点的小木块A以速度v0＝0.2，由滑板B左端开始沿滑板B表面向右运动．已知A的质量m=1kg，g取10m/s2 ．求：

    （1）弹簧被压缩到最短时木块A的速度；

    （2）木块A压缩弹簧过程中弹簧的最大弹性势能．

    查看答案和解析>>

    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，其右端固定一根水平轻质弹簧，弹簧的自由端C互滑板左端的距离L=0.5m，这段滑板与木块A（可视为质点）之间的动摩擦因数，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。小木块A以速度v0=10m/s由滑板B左端开始沿滑板的水平面上表面向右运动。已知木块A的质量m=1kg,g取10m/s2。求：

    ①弹簧被压缩到最短时木块A的速度；

    ②木块A压缩弹簧过程中弹簧弹势能最大值。

    查看答案和解析>>

    如图所示，质量M=4Kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，这段滑板与木块A之间的动摩擦因数，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。可视为质点的小木块A质量m=1Kg，原来静止于滑板的左端，当滑板B受水平向左恒力F=14N，作用时间t后撤去F，这时木块A恰好到达弹簧自由端C处，假设A、B间的最大静摩擦力和滑动摩擦力相等，g取10，求：
    （1）水平恒力F的作用时间t；
    （2）木块A压缩弹簧过程中弹簧的最大弹性势能。

    查看答案和解析>>

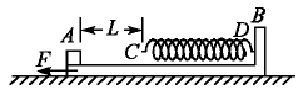
    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，可视为质点的小木块A质量m=1kg，原来静止于滑板的左端，滑板与木块A之间的动摩擦因数μ=0.2．当滑板B受水平向左恒力F=14N作用时间t后，撤去F，这时木块A恰好到达弹簧自由端C处，此后运动过程中弹簧的最大压缩量为s=5cm．g取10m/s2．  

       求：（1）水平恒力F的作用时间t；

    （2）木块A压缩弹簧过程中弹簧的最大弹性势能；

    （3）当小木块A脱离弹簧且系统达到稳定后，整个运动过程中系统所产生的热量．


    查看答案和解析>>

    一.选择题

    1．C 

    2．D  

    3．C   

    4．B  

    5．B  

    6．C  

    7．D  

    8．C 

    9. AD

     10. AC

    二．实验题（18分）

    11．①4.4N至5.2N均给分（2分）（图2分，从略）  ②只用一个弹簧称将橡皮条的节点拉到同一位置O点（2分），弹簧称的示数，拉力的方向（每空1分）

    12．①C，E（4分）②b（2分）③ 图4分，从略，有错误就不给分

    三.计算题

    13．(1)弹簧被压缩到最短时，木块A与滑板B具有相同的速度，设为V，从木块A开始沿滑板B表面向右运动至弹簧被压缩到最短的过程中，A、B系统的动量守恒：

    mV0＝(M+m)V                             ①

                                 ②

    木块A的速度：V＝2m/s                    ③

    (2)木块A压缩弹簧过程中，弹簧被压缩到最短时，弹簧的弹性势能最大。

    　由能量关系，最大弹性势能：

    　      ④

    　EP＝39J                                ⑤

    评分标准：本题15分．①、②式各4分，③式2分；④式3分，⑤式2分．

    14．棒在0时刻受到拉力F和摩擦力f的作用,此时的加速度等于直线AO的斜率.据牛顿第二定律                    ①

    又                   ②

    由以上两式得                  ③

    设当棒达到最大速度v时,电动势为E,电流为I,棒受到的安培力为F安,则

      ④             ⑤           ⑥

    此时棒处在平衡状态           ⑦

    由③--⑦得                      ⑧

    (1)   电阻上产生的热量等于过程中导体棒克服安培力所的功W

    对棒应用动能定理    ⑨

    带入数据得                     ⑩

    过程中电阻上产生的热量为20J

    评分标准: 共17分,②③⑤⑧式各1分,其余每式2分

    15.⑴旋转后电子的初速度与地磁场的方向垂直，受到向下的洛仑兹力，在与地磁场垂直的平面内沿圆弧运动，Ｓ′应在Ｓ的正下方．

    ⑵旋转后，电子的运动轨迹如图所示，设轨道半径为Ｒ

    （R－b）2＋a2=R2                 ①

    电子经加速电场所获得的速度为v

    eU=mv2　　　　　　　　　　　　②

    洛仑兹力提供做圆周运动的向心力，高地磁场磁感应强度大小为Ｂ

    Ｂev=m　　　　　　　　　　　　③

    由以上三式解得

    B=　　　　　　　　④

     

     

     


    同步练习册答案