
题目列表(包括答案和解析)
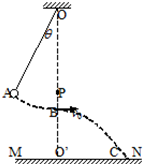 利用单摆验证小球平抛运动规律,设计方案如图所示,在悬点O正下方有水平放置的炽热的电热丝P,当悬线摆至电热丝处时能轻易被烧断;MN为水平木板,已知悬线长为L,悬点到木板的距离OO′=h(h>L).
利用单摆验证小球平抛运动规律,设计方案如图所示,在悬点O正下方有水平放置的炽热的电热丝P,当悬线摆至电热丝处时能轻易被烧断;MN为水平木板,已知悬线长为L,悬点到木板的距离OO′=h(h>L).
|
|

|
|
(1)电热丝P必须放在悬点正下方的理由是:____________.


(2)将小球向左拉起后自由释放,最后小球落到木板上的C点,O'C=s,则小球做平抛运动的初速度为v0=________.
(3)在其他条件不变的情况下,若改变释放小球时悬线与竖直方向的夹角q,小球落点与O'点的水平距离s将随之改变,经多次实验,以s2为纵坐标、cosq为横坐标,得到如图(b)所示图像.则当q=30°时,s为 ________m;若悬线长L=1.0m,悬点到木板间的距离OO'为________m.

(1)电热丝户必须放在悬点正下方的理由是:_______________________________________;
(2)将小球向左拉起后自由释放,最后小球落到木板上的C点,O′C=s,则小球做平抛运动的初速度v0为______________;
(3)若其他条件不变的情况下,改变释放小球时悬线与竖直方向的夹角θ,小球落点与O′点的水平距离s将随之改变,经多次实验,以s2为纵坐标、cosθ为横坐标,得到如图乙所示图象.则当θ=30°时,s为___________m;若悬线长L=1.
利用单摆验证小球平抛运动规律,设计方
案如图(a)所示,在悬点O正下方有水平放置的炽热的电热丝P,当悬线摆至电热丝处时能轻易被烧断;MN为水平木板,已知悬线长为L,悬点到木板的距离OO/=h(h>L)。
⑴电热丝P必须放在悬点正下方的理由是:________ ____。
⑵将小球向左拉起后自由释放,最后小球落到木板上的C点,O/C=s,则小球做平抛运动的初速度为v0=________。
⑶在其他条件不变的情况下,若改变释放小球时悬线与竖直方向的夹角q,小球落点与O/点的水平距离s将随之改变,经多次实验,以s2为纵坐标、cosq为横坐标,得到如图(b)所示图像。则当q=23°时,s为________m;若悬线长L=1.0 m,悬点到木板间的距离OO/为________m。(cos230=0.92)
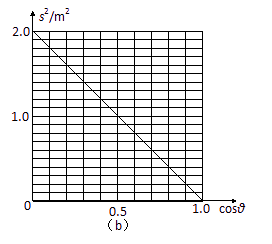
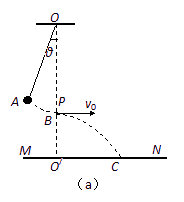
一.选择题
1.C
2.D
3.D
4.D
5.A
6.C
7. AC
8. B
9.AC
10.C
二.实验题
11 . 1.(1)×100;(2分)(2)T;(2分)
2.20kΩ;(2分)
3.(1)
①按电路图连接好电路。
②将开关S与1连接。读出此时电流表示数。
③将电阻箱调为最大,然后将S与2连接,调节电阻箱的阻值,使电流表的示数与步骤(2)中电流表示数相同。读出此时电阻箱的阻值R,则被测电阻Rx=R
④断开电路整理好器材
(每空1分;顺序颠倒但合理同样给分。)
(2)实物图连接略(2分)
12.(1)保证小球沿水平方向抛出(2分) (2)(2分)(3)0.52(2分)
三.计算题:
13.解析:设弹簧的弹性势能为 E,小球的质量为 m,小球在空中运动的时间为 t,第一次弹出时小球的速度为 v 。
则有
.files/image032.gif) ① (2分)
① (2分)
运动的水平距离
.files/image034.gif) ② (1分)
② (1分)
设第二次弹出时小球的速度为 v1 ,小车的速度为 v2
则有
.files/image036.gif) ③ (2分)
③ (2分)
且
.files/image038.gif) ④ (2分)
④ (2分)
而
.files/image040.gif) ⑤ (2分)
⑤ (2分)
由①、②、③、④、⑤得 .files/image042.gif) (1分)
(1分)
14.解析:(1)切割磁感线的速度为v,任意时刻线框中电动势大小
.files/image044.gif) ,(4分) 导线中的电流大小
,(4分) 导线中的电流大小
.files/image046.gif) (4分)
(4分)
(2)线框所受安培力的大小和方向
.files/image048.gif) (4分) 由左手定则判断、线框所受安培力的方向始终沿x轴正方向.
(4分) 由左手定则判断、线框所受安培力的方向始终沿x轴正方向.
.files/image050.jpg) 15.解:(1)带负电粒子射入磁场后,由于受到洛伦兹力的作用,粒子将沿图示的轨迹运动,从A点射出磁场,设O、A间的距离为L,射出时速度的大小仍为v,射出方向与x轴的夹角仍为θ,由洛伦兹力公式和牛顿定律可得:
15.解:(1)带负电粒子射入磁场后,由于受到洛伦兹力的作用,粒子将沿图示的轨迹运动,从A点射出磁场,设O、A间的距离为L,射出时速度的大小仍为v,射出方向与x轴的夹角仍为θ,由洛伦兹力公式和牛顿定律可得:
qv0B=m.files/image052.gif) (1分)
(1分)
式中R为圆轨道半径,解得:
R=.files/image054.gif) (2分)
(2分)
圆轨道的圆心位于OA的中垂线上,由几何关系可得:
.files/image056.gif) =Rsinθ (2分)
=Rsinθ (2分)
联解①②两式,得:L=.files/image058.gif) (2分)
(2分)
所以粒子离开磁场的位置坐标为(-.files/image058.gif) ,0)(2分)
,0)(2分)
(2)因为T=.files/image061.gif) =
=.files/image063.gif) (2分)
(2分)
所以粒子在磁场中运动的时间,t=.files/image065.gif) (2分)
(2分)
16.解析:(1)设带电橡胶棒刚好全部进入“U”形框架时,达到与“U”形框架共速v,则由动能定理:.files/image067.gif) ……………………………………①
……………………………………①
由动量守恒:mv0=(m+M)v………………………………………………………②
其中E=.files/image069.gif) ………………………………………………………………………③
………………………………………………………………………③
由①②③式联立得:L=0.3125(m)
∴L>l………………………………………………………………………………④
橡胶棒能全部进入“U”形框架.
(2)设相互作用过程中“U”形框架的最终速度为v2,棒的最终速度为v1
由(1)知棒能全部穿出“U”形框架
由动能定理:2×.files/image071.gif) ………………………………⑤
………………………………⑤
由动量守恒:mv0=mv1+Mv2 ……………………………………………………⑥
由③⑤⑥式联立得:v2=
(3)系统增加的电势能等于机械能的减小量
△E=.files/image073.gif) (J) ……………………………………………⑧
(J) ……………………………………………⑧
评分标准:本题共18分,①②③④⑤⑥⑦⑧式各1分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com