
题目列表(包括答案和解析)
 如图甲,将一质量为0.4kg的足够长的绝缘均匀细管置于光滑水平地面上,管的内表面粗糙.有一质量为0.1kg,带电量为0.1C的带正电小球沿细管轴线方向以一定速度向右进入管内,细管内径略大于球的直径,空间存在如如图所示的匀强磁场,磁感应强度
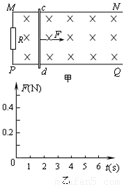
如图甲,将一质量为0.4kg的足够长的绝缘均匀细管置于光滑水平地面上,管的内表面粗糙.有一质量为0.1kg,带电量为0.1C的带正电小球沿细管轴线方向以一定速度向右进入管内,细管内径略大于球的直径,空间存在如如图所示的匀强磁场,磁感应强度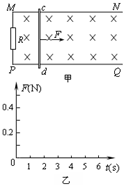 如图甲所示,MN、PQ为水平放置的足够长的平行光滑导轨,导轨间距L为0.5m,导轨左端连接一个2Ω的电阻R,将一根质量m为0.4kg的金属棒c d垂直地放置导轨上,且与导轨接触良好,金属棒的电阻r大小为0.5Ω,导轨的电阻不计,整个装置放在磁感强度B为1T的匀强磁场中,磁场方向垂直于导轨平面向下,现对金属棒施加一水平向右的拉力F,使棒从静止开始向右运动.当棒的速度达到1m/s时,拉力的功率为0.4w,此刻t=0开始计时并保持拉力的功率恒定,经一段时间金属棒达到稳定速度,在该段时间内电流通过电阻R做的功为1.2J.试求:
如图甲所示,MN、PQ为水平放置的足够长的平行光滑导轨,导轨间距L为0.5m,导轨左端连接一个2Ω的电阻R,将一根质量m为0.4kg的金属棒c d垂直地放置导轨上,且与导轨接触良好,金属棒的电阻r大小为0.5Ω,导轨的电阻不计,整个装置放在磁感强度B为1T的匀强磁场中,磁场方向垂直于导轨平面向下,现对金属棒施加一水平向右的拉力F,使棒从静止开始向右运动.当棒的速度达到1m/s时,拉力的功率为0.4w,此刻t=0开始计时并保持拉力的功率恒定,经一段时间金属棒达到稳定速度,在该段时间内电流通过电阻R做的功为1.2J.试求: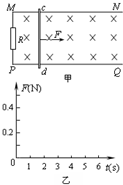
一.选择题
1.B 2.D 3.B 4.AC 5.B 6.D 7.D 8.C 9. BD 10.A
二.实验题(共18分)
11.甲 乙(5分) 12.①Rg=90Ω (2分),偏小(2分) ②(1).略(5分),(2).R(2分) ,Rs(2分)
三.计算题
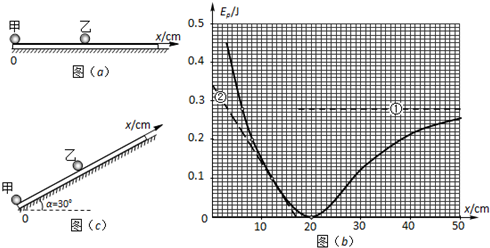
13.(共16分)(1) 分析判断当F= 8N时,设小物块的加速度为a,则
a = .files/image026.gif)
因此小物块先作加速度较大的匀加速直线运动,之后与小车一起做加速度较小的匀加速直线运动。设开始时小物块的加速度为a1,小车的加速度为a2,与小车共同的加速度为a3,两物体达到共同速度的时间为t,则 .files/image028.gif)
且
.files/image030.gif)
.files/image032.gif)
.files/image034.gif)
由以上各式得:
.files/image036.gif)
S =
(2) 与(1)同理,但小物块一直作匀加速直线运动,解得:S=
14.解析。如图选坐标,斜面的方程为:
.files/image038.jpg)
.files/image040.gif) ①(2分)
①(2分)
运动员飞出后做平抛运动
.files/image042.gif) ②(1分)
②(1分)
.files/image044.gif) ③(1分)
③(1分)
联立①②③式,得飞行时间 t=1.2 s (1分)
落点的x坐标:x1=v0t=
落点离斜面顶端的距离:.files/image046.gif) (2分)
(2分)
落点距地面的高度:.files/image048.gif) (2分)
(2分)
接触斜面前的x分速度:.files/image050.gif) (1分)
(1分)
y分速度:.files/image052.gif) (1分)
(1分)
沿斜面的速度大小为:.files/image054.gif) (2分)
(2分)
设运动员在水平雪道上运动的距离为s2,由功能关系得:
.files/image056.gif) (2分)
(2分)
解得:s2=
15.(共18分)(1)如右图(6分)
(2)假设小球细管与能相对静止:mv0=(M+m)v′ (3分)
得:v′=
由(1)问分析可知,当球的速度为
mv0=Mv2+mv1 (3分) 则: v2=
内能Q=mv02-mv12+Mv22=13.75J(2分)
.files/image058.jpg)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com