0000——青夏教育精英家教网—

0000 【查看更多】

某校物理兴趣小组设计一个玻璃管测力计：横截面积

次数	1	2	3	4
m/Kg	0.000	0.100	0.250
L/cm	2.00	2.22		3.36

S=1﹒00cm²的一端封闭、一端开口的玻璃管内，一个很薄的轻质活塞封闭了一定量的空气，活塞连结一个秤钩．将测力计开口向下竖直悬挂，下端秤钩挂上砝码，如图所示．现将不同质量的砝码m挂在秤钩上，稳定后用刻度尺测量出活塞与管顶之间的距离L，在实验过程中，气体的温度保持不变，四次实验部分数据记录在下面的表格上：
（1）通过计算，将数据填入表内两个空白处．
实验时大气压强P=______帕．（用科学记数法表示，保留三位有效数字，即其系数计算到小数点后两位）
在玻璃管测力计上L=4.00cm处应标上所测作用力大小F=______N．空气柱长度L随加在秤钩上作用力F变化而______（填：均匀，不均匀）变化．
（2）通过实验，同学们发现用玻璃管测力计来测力，还存在一些不足之处，其中主要的不足之处①______；②______．

查看答案和解析>>

某校物理兴趣小组设计一个玻璃管测力计：横截面积

次数	1	2	3	4
m/Kg	0.000	0.100	0.250
L/cm	2.00	2.22		3.36

S=1﹒00cm²的一端封闭、一端开口的玻璃管内，一个很薄的轻质活塞封闭了一定量的空气，活塞连结一个秤钩．将测力计开口向下竖直悬挂，下端秤钩挂上砝码，如图所示．现将不同质量的砝码m挂在秤钩上，稳定后用刻度尺测量出活塞与管顶之间的距离L，在实验过程中，气体的温度保持不变，四次实验部分数据记录在下面的表格上：
（1）通过计算，将数据填入表内两个空白处．
实验时大气压强P=______帕．（用科学记数法表示，保留三位有效数字，即其系数计算到小数点后两位）
在玻璃管测力计上L=4.00cm处应标上所测作用力大小F=______N．空气柱长度L随加在秤钩上作用力F变化而______（填：均匀，不均匀）变化．
（2）通过实验，同学们发现用玻璃管测力计来测力，还存在一些不足之处，其中主要的不足之处①______；②______．

查看答案和解析>>

表格中所列数据是测量小灯泡 U-I关系的实验数据：

U/V	0.0	0.2	0.5	1.0	1.5	2.0	2.5	3.0
I/A	0.000	0.050	0.100	0.150	0.180	0.195	0.205	0.215

（1）分析上表内实验数据可知，应选用的实验电路图（图14-8-10）是图____（填“甲”或“乙”）；

图14-8-10

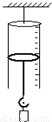
（2）在图14-8-11中画出小灯泡的U-I曲线.分析曲线可知小灯泡的电阻随I的变大而_____（填“变大”“变小”或“不变”）；

图14-8-11

（3）如图丙所示，用一个定值电阻R和两个上述小灯泡组成串并联电路，连接到内阻不计、电动势为3 V的电源上.已知流过电阻R的电流是流过灯泡b电流的两倍，则流过灯泡b的电流约为_______A.

查看答案和解析>>

表格中所列数据是测量小灯泡U-I关系的实验数据：

U/V	0.0	0.2	0.5	1.0	1.5	2.0	2.5	3.0
I/A	0.000	0.050	0.100	0.150	0.180	0.195	0.205	0.215

(1)分析上表内实验数据可知，应选用的实验电路图是图14-26中的________(填“甲”或“乙”)；

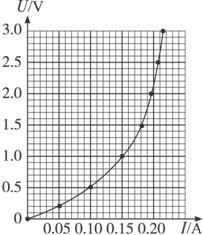
图14-26

(2)在方格纸内画出小灯泡U-I曲线.分析曲线可知小灯泡的电阻随I变大而_______(填“变大”“变小”或“不变”)；

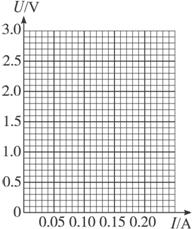
图14-27

(3)如图丙所示，用一个定值电阻R和两个上述小灯泡组成串并联电路，连接到内阻不计、电动势为3 V的电源上.已知流过电阻R的电流是通过灯泡b电流的两倍，则流过灯泡b的电流约为____________A.

查看答案和解析>>

表格中所列数据是测量小灯泡U-I关系的实验数据：

U/V	0.0	0.2	0.5	1.0	1.5	2.0	2.5	3.0
I/A	0.000	0.050	0.100	0.150	0.180	0.195	0.205	0.215

（1）分析上表内实验数据可知，应选用的实验电路图是下图中的__________（填“甲”或“乙”）；

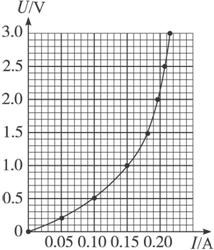
（2）在下图所示的方格纸内画出小灯泡的U-I曲线.分析曲线可知小灯泡的电阻随I变大而__________（填“变大”“变小”或“不变”）；

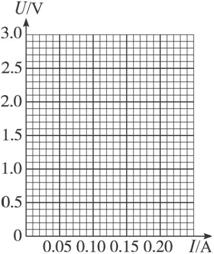
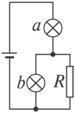
（3）如图所示，用一个定值电阻R和两个上述小灯泡组成串并联电路，连接到内阻不计、电动势为3 V的电源上.已知流过电阻R的电流是流过灯泡b电流的两倍，则流过灯泡b的电流约为__________ A.

查看答案和解析>>

一．选择题

1.C

2.D

3.BD

4.D

5.C

6.D

7.B

8.A

9. AD

10.AD

二．实验题

11．（1）如图所示（5分）

（2）9．95（9.90---9.99范围内均给分）（5分）

12．（1）ADCBE（2分）

（2）1.735（3分）

（3）576.9 (577同样给分)（3分）

三．计算题（52分）

13．（18分）参考解答：

电子穿过电容器过程中，在水平方向上做匀速运动 ① （1分）

在竖直方向上做匀加速直线运动 ② （2分）

v_⊥=at ③ （1分）

a= ④ （2分）

电子穿过平行板电容器时，速度方向偏转θ角， tanθ= ⑤ （2分）

电子打在荧光屏上偏离中心O的位移，y=y₁+s?tanθ （2分）

由上述①～⑥方程得：y=（1+）y₁

当y₁=d/2时，代入数据求得：y=3m> ⑦ （1分）

故使电子打在荧光屏上，应满足y≤阶段（1分）

联立①～⑦方程，

代入数据求得，A、B间电压U≤25V （2分）

⑴当U_AB=25V时，

代入数据得：R₃=900Ω （1分）

⑵当U_BA=25V时，

代入数据得：R₃=100Ω （1分）

综述： 100Ω≤R₃ ≤900Ω （2分）

14．（16分）参考解答：

⑴设每个人对夯锤施加的力用F表示，根据牛顿第二定律有：

………………………………………………………⑴

施力过程中夯锤上升的高度为h₁，松手时夯锤获得的速度为v，松手后夯锤能上升的高度为h₂_，夯锤能上升的最大高度为h，根据运动规律有：

……………………………………………………………⑵

…………………………………………………………………⑶

………………………………………………………………⑷

……………………………………………………………⑸

代入数值后可解得： ………………………………………………⑹

⑵设夯锤与地面撞击的过程中，地面对夯锤的平均作用力为N，研究夯锤从最高点至落到地面的过程，应用动能定理可得：

……………………………………………⑺

将Δh=0.02及第⑴问所得结果代入上式可得：

N=2.33×10⁴N …………………………………………⑻

根据牛顿第三定律，此即等于夯锤对地面的平均作用力．

本题满分16分，每式2分。注：其它解法结果正确同样给分。

15．（20分）参考解答：

（1）木箱在水平恒力和滑动摩擦力f₁ 的作用下，由静止开始做匀加速直线运动，加速度为a₁，金属块在光滑木箱上表面处于静止，直到木箱向前前进1 m后，金属块滑落，做自由落体运动，竖直落到地面。滑动摩擦力f₁=μ(M+m)g= 8 N (2分)

由牛顿运动定律得：a₁=（F―f₁）/M =0.5m/s² (2分)

木箱滑行1m，历时 t₁==2s (2分)

金属块滑落后，木箱在水平恒力和滑动摩擦力f₂ 的作用下，做匀加速直线运动1s，加速度为a₂，滑动摩擦力f₂=μMg= 5 N (1分)

由牛顿运动定律得：a₂=（F―f₂）/M =2m/s² (2分)

2s末木箱的速度为v₁=a₁t₁=1m/s (2分)

第3s内的位移s₂=v₁t₂+=2m (2分)

3s末木箱的速度为v₂= v₁+a₂t₂=3m./s (2分)

撤去力F后，木箱做匀减速运动直至停止，减速运动的加速度a3= ―μg =―2.5 m/s² (1分)

此过程的位移S3= =1.8m (2分)

因此木箱停止后，小金属块落地点距木箱左边沿的水平距离 S=S₂=S₃=3.8m (2分)

练习册

高中

初中

小学