
题目列表(包括答案和解析)
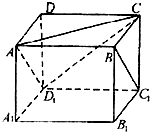 (A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:
(A题)如图正方体ABCD-A1B1C1D1,则下列四个命题: (A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:
(A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:设抛物线 :
: (
( >0)的焦点为
>0)的焦点为 ,准线为
,准线为 ,
, 为
为 上一点,已知以
上一点,已知以 为圆心,
为圆心, 为半径的圆
为半径的圆 交
交 于
于 ,
, 两点.
两点.
(Ⅰ)若 ,
, 的面积为
的面积为 ,求
,求 的值及圆
的值及圆 的方程;
的方程;
(Ⅱ)若 ,
, ,
, 三点在同一条直线
三点在同一条直线 上,直线
上,直线 与
与 平行,且
平行,且 与
与 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到 ,
, 距离的比值.
距离的比值.
【命题意图】本题主要考查圆的方程、抛物线的定义、直线与抛物线的位置关系、点到直线距离公式、线线平行等基础知识,考查数形结合思想和运算求解能力.
【解析】设准线 于
于 轴的焦点为E,圆F的半径为
轴的焦点为E,圆F的半径为 ,
,

则|FE|= ,
, =
= ,E是BD的中点,
,E是BD的中点,
(Ⅰ) ∵ ,∴
,∴ =
= ,|BD|=
,|BD|= ,
,
设A( ,
, ),根据抛物线定义得,|FA|=
),根据抛物线定义得,|FA|= ,
,
∵ 的面积为
的面积为 ,∴
,∴ =
= =
= =
= ,解得
,解得 =2,
=2,
∴F(0,1), FA|= , ∴圆F的方程为:
, ∴圆F的方程为: ;
;
(Ⅱ) 解析1∵ ,
, ,
, 三点在同一条直线
三点在同一条直线 上, ∴
上, ∴ 是圆
是圆 的直径,
的直径, ,
,
由抛物线定义知 ,∴
,∴ ,∴
,∴ 的斜率为
的斜率为 或-
或- ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
设直线 的方程为:
的方程为: ,代入
,代入 得,
得, ,
,
∵ 与
与 只有一个公共点,
∴
只有一个公共点,
∴ =
= ,∴
,∴ ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
∴坐标原点到 ,
, 距离的比值为3.
距离的比值为3.
解析2由对称性设 ,则
,则
点 关于点
关于点 对称得:
对称得:
得: ,直线
,直线
 切点
切点
直线
坐标原点到 距离的比值为
距离的比值为
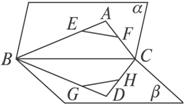
如图.五角星魅力无穷,移动点由A处按图中数字由小到大的顺序依次运动,当第一次结束回到A处时,数字为6,按此规律无限运动,则数字2010应在
A. B处 B. C处 C. D处 D. E处
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com