
题目列表(包括答案和解析)
关于函数![]() ,有下列命题:
,有下列命题:
①由![]() ,可得
,可得![]() 必是π的整数倍;
必是π的整数倍;
②若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ;
;
③函数y=f(x)的图像关于点![]() 对称;
对称;
④函数y=f(-x)的单调递增区间可由不等式![]() 求得.
求得.
其中正确命题的序号是________(把你认为正确的命题的序号都填上).
已知向量 =(
=( ),
), =(
=(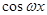 ,
,
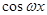 ),其中(
),其中(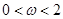 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 .
.
(I)求函数 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
【解析】第一问利用向量的数量积公式表示出
 ,然后利用
,然后利用 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
解:因为

由余弦定理得 ,……11分故
,……11分故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com