
题目列表(包括答案和解析)
(09年东城区二模理)(14分)
已知函数![]() =
=![]() (其中
(其中![]() 为常数,
为常数,![]() ).利用函数
).利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:
,方法如下:
对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述构造过程中,如果![]() (
(![]() =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果![]() 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(Ⅰ)当![]() 且
且![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(Ⅱ)如果可以用上述方法构造出一个常数列,求![]() 的取值范围;
的取值范围;
(本小题满分14分)
已知函数![]() 对于任意
对于任意![]() (
(![]() ),都有式子
),都有式子![]() 成立(其中
成立(其中![]() 为常数).
为常数).
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)利用函数![]() 构造一个数列,方法如下:
构造一个数列,方法如下:
对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述构造过程中,如果![]() (
(![]() =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果![]() 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(ⅰ)如果可以用上述方法构造出一个常数列,求![]() 的取值范围;
的取值范围;
(ⅱ)是否存在一个实数![]() ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为![]() ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(ⅲ)当![]() 时,若
时,若![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
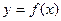 对于任意
对于任意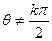 (
(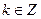 ),都有式子
),都有式子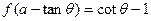 成立(其中
成立(其中 为常数).
为常数).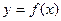 的解析式;
的解析式; 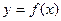 构造一个数列,方法如下:
构造一个数列,方法如下: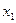 ,令
,令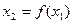 ,
,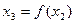 ,…,
,…,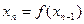 ,…
,… 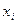 (
(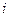 =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果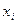 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止. 的取值范围;
的取值范围; ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为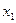 ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列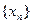 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;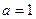 时,若
时,若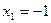 ,求数列
,求数列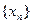 的通项公式.
的通项公式. (其中a为常数,x≠a).利用函数y=f(x)构造一个数列{xn},方法如下:
(其中a为常数,x≠a).利用函数y=f(x)构造一个数列{xn},方法如下:已知函数y=f(x)对于任意![]() (k∈Z),都有式子f(a-tanθ)=cotθ-1成立(其中a为常数).
(k∈Z),都有式子f(a-tanθ)=cotθ-1成立(其中a为常数).
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)利用函数y=f(x)构造一个数列,方法如下:
对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述构造过程中,如果xi(i=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果xi不在定义域中,那么构造数列的过程就停止.
(ⅰ)如果可以用上述方法构造出一个常数列,求a的取值范围;
(ⅱ)是否存在一个实数a,使得取定义域中的任一值作为x1,都可用上述方法构造出一个无穷数列{xn}?若存在,求出a的值;若不存在,请说明理由;
(ⅲ)当a=1时,若x1=-1,求数列{xn}的通项公式.
一、选择题
1―8 DAACA CBD
二、填空题
9. 10.
10. 11.
11. 12.
12. 13.50 14.5
13.50 14.5
三、解答题
15.(本小题满分13分)
解:(1)由 ………………2分
………………2分
整理得
即 ……………………3分
……………………3分
又 ……………………5分
……………………5分
又因为 ,
,
所以 …………………………6分
…………………………6分
(2)因为 ,所以
,所以
故 …………………………7分
…………………………7分
由
即 ,
,
所以 .
.
即 .……………………11分
.……………………11分
因为 ……………………12分
……………………12分
故
所以 ……………………13分
……………………13分
16.(本小题满分13分)
解:(1)取AC的中点O,连结OS,OB。
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥OB。又平面SAC⊥平面ABC,且平面SAC∩平面ABC=BC,
∴SO⊥平面ABC。
故SB在平面ABC内的射影为OB。
∴AC⊥SB.……………………6分
(2)取OB的中点D,作NE⊥CM交GM于E,连结DE,ND。
在△SOB中,N、D分别为SB,OB的中点,
∴DN//SO,又SO⊥平面ABC,
∴DN⊥平面ABC,由NE⊥CM得DE⊥CM。
故∠NED为二面角N―CM―B的平面角,………………9分
设OB与CM交于G,则G为△ABC的中心
∴ DE⊥CM,BM⊥CM,
DE⊥CM,BM⊥CM,
|