
题目列表(包括答案和解析)
(本题满分14分)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证: ≤bn<2.
≤bn<2.
(本题满分14分)已知函数f (x)=lnx,g(x)=ex.
(I)若函数φ (x) = f (x)- ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(Ⅱ)设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
注:e为自然对数的底数.
(本题满分14分)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .(I)求数列{an}的通项公式;
.(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
(本题满分14分)已知函数 (
(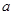 是常数)
是常数)
(I) 求函数 的单调区间;
的单调区间;
(II) 当 在
在 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数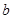 的取值范围;
的取值范围;
(III) 求证:当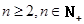 时
时 .
.
(本题满分14分)已知函数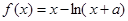 (
( 是常数)
是常数)
(I) 求函数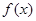 的单调区间;
的单调区间;
(II) 当 在
在 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数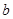 的取值范围;
的取值范围;
(III) 求证:当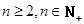 时
时 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com