
题目列表(包括答案和解析)
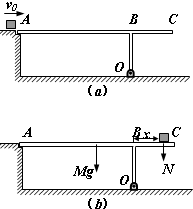 如图(a)所示,ABCO是固定在一起的T型支架,其中水平部分AC是质量为M=2kg、长度为L=1m的匀质薄板,OB是轻质硬杆,下端通过光滑铰链连接在水平地面上,可绕水平轴O在竖直面内自由转动,支架A端搁在左侧平台上.已知AB的长度l1=
如图(a)所示,ABCO是固定在一起的T型支架,其中水平部分AC是质量为M=2kg、长度为L=1m的匀质薄板,OB是轻质硬杆,下端通过光滑铰链连接在水平地面上,可绕水平轴O在竖直面内自由转动,支架A端搁在左侧平台上.已知AB的长度l1=| 3 |
| 4 |
| L |
| 2 |
| 3 |
| 4 |
第一问 车和物体收到的力都是摩擦力
f=μmg 车的加速度a1=f/M=μmg/M=1m/s^2
滑块的加速度a2=f/m=μmg/m=5m/s^2
第二问 S=2.7m
假设不能从车上滑出 那么滑块最后必定停留在车上 并且和车具有同样的末速度 设为v'
因为系统在水平方向上所受的合外力为零 所以满足动量守恒
Mv+mv0=(M+m)*v' → v'=v0*m/(M+m)=7.5*10/(10+50)=1.25m/s
然后我们看能量 如果系统的初动能减去末动能 小于摩擦力所能做的最大功(就是滑块滑到头 但没掉下来) 那么假设成立 反之 不成立 不能明白的话 我们看下面具体的解答
先求系统的末动能 Ek'=1/2(M+m)v'^2=1/2*(50+10)*1.25^2=46.875(J)
系统的初动能 Ek=1/2mv0^2=1/2*10*7.5^2=281.25(J)
摩擦力所能做的最大功 W=fs=μmgs=0.5*10*10*3=150(J)
Ek-Ek'>W 所以也就是说 系统的初动能被摩擦力消耗掉一部分后【克服摩擦力做功】 所剩下的动能 还是要大于他们最后一起以同样的速度运动时的动能 因此滑块最后不肯能停在车上
那么 我们就来求滑块落地时与平板车右端间的水平距离
因为滑块滑出小车后 在水平方向上和小车都是做匀速运动
所以他们之间的距离 就是他们的速度差乘以滑块落地所需的时间
那么 我们就需要算出滑块的末速度v'和小车的末速度v''
现在有两个未知数 那就必须有两个方程
第一个方程是能量方程 Ek-W=1/2mv'^2+1/2Mv''^2
第二个方程是动量方程 mv0=mv'+Mv''
联立这两个方程 解得 v''=0.5m/s 或 v''=2m/s(舍掉)
从而得到v'=5m/s
接下来算滑块落地要多长时间
由h=1/2gt^2 带入数据 得t=0.6s
所以最后的答案: S=(v'-v'')*t=4.5*0.6=2.7m
(1)在t=0时刻,质点A开始做简谐运动,其振动图象如图甲所示.
质点A振动的周期是________s;t=8 s时,质点A的运动沿y轴的________方向(填“正”或“负”);质点B在波的传播方向上与A相距16 m.已知波的传播速度为2 m/s,在t=9 s时,质点B偏离平衡位置的位移是________ cm.
(2)图乙是北京奥运会期间安置在游泳池底部的照相机拍摄的一张照片,相机的镜头竖直向上.照片中,水立方运动馆的景象呈现在半径r=11 cm的圆形范围内,水面上的运动员手到脚的长度l=10 cm.若已知水的折射率n=,请根据运动员的实际身高估算该游泳池的水深h.(结果保留两位有效数字)
【解析】:(1)由图知T=4s,因位移图线的斜率表示速度,且在t=8 s=2T时质点振动状态与t=0时相同,则由图可知t=0时图线斜率为正,速度沿y轴正向.在t=9 s时由图线知质点A处于正向最大位移处.再由Δt==8s=2T知B的振动状态与质点A相差两个周期,所以同一时刻两质点相对平衡位置的位移相同,即也为10 cm.
图10
(2)设照片圆形区域的实际半径为R,运动员的实际长为L
由折射定律nsinα=sin90°
几何关系sinα=,=
得h=·r
取L=2.2 m,解得h=2.1 m(1.6~2.6 m都算对)
| l |
| 2 |
| l |
| 2 |
| 1 |
| 2 |
| d |
| l |



| 代表符号 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 刻度数值/cm | 0.85 | 1.7 | 2.55 | 4.3 | 5.10 | 6.00 |

| d1+d2+d3+d4 |
| 4 |
| d1+d2+d3+d4 |
| 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com