
题目列表(包括答案和解析)
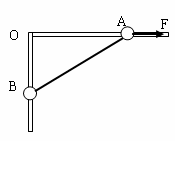
如图所示,竖置平面内放一光滑直角杆,水平、竖直两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B, A、B间用不可伸长的轻绳相连,初始位置为OA=1.5m,OB=2.0m.g取10m/s2.
(1)若用水平力F1沿杆向右拉A,使A由初始位置向右极缓慢地移动0.5 m,则该过程中拉力F1做了多少功?
(2)若用水平力F2沿杆向右拉A,使B以1m/s的速度匀速上升,则在B从初始位置上升0.5 m的过程中,拉力F2做了多少功?
如图所示,竖置平面内放一光滑直角杆,水平、竖直两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B, A、B间用不可伸长的轻绳相连,初始位置为OA=1.5m,OB=2.0m.g取10m/s2.
(1)若用水平力F1沿杆向右拉A,使A由初始位置向右极缓慢地移动0.5 m,则该过程中拉力F1做了多少功?
(2)若用水平力F2沿杆向右拉A,使B以1m/s的速度匀速上升,则在B从初始位置上升0.5 m的过程中,拉力F2做了多少功?
 如图所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2m 的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动.质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生弹性碰撞. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为μ=0.5,A、B、C 均可视为质点,重力加速度为g.
如图所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2m 的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动.质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生弹性碰撞. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为μ=0.5,A、B、C 均可视为质点,重力加速度为g.| 1 | 3 |
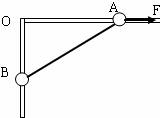
 如图所示,竖直平面内放置一直角杆AOB,杆的水平部分粗糙,竖直部分光滑,两部分各有质量相等的小球A和B套在杆上,A、B间用轻绳相连,以下说法中正确的是( )
如图所示,竖直平面内放置一直角杆AOB,杆的水平部分粗糙,竖直部分光滑,两部分各有质量相等的小球A和B套在杆上,A、B间用轻绳相连,以下说法中正确的是( )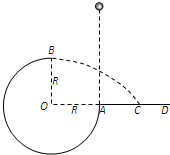 如图所示,竖直平面内的 3/4 圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求:
如图所示,竖直平面内的 3/4 圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求:一、单选题:
1.B 2.B. 3.A 4.C 5.D 6.B
二、多选题:
7.BD 8.ABD 9.AC 10.CD 11.AC
三、填空题:
12.S1、S6 ;S1、S2、S3、S4、S5、S6 , B .纸带运动时受到打点计时器的阻力,测量计数点之间的距离时会有测量误差.
13.(1)斜槽末端水平, 保持小球水平抛出的初速度相同.(2)保持相邻痕迹点的水平距离大小相同 .(3)略
四、计算或论述题:
14.Fcos =
= (mg-Fsin
(mg-Fsin )
)
F(cos +
+ sin
sin )=
)= mg ①
mg ①
F=kx ②
联立解出:k=
15.原题解法不合理。正确解法为:设加速、减速时间分别为t1、t2
由题意得: ①
①
 ②
②
代入数据联立求解得到t1=9s、t2=2s
且途中实际最大速度 =
=
16.解:(1)设土星质量为M0,颗粒质量为m,颗粒距土星中心距离为r,线速度为v,
根据牛顿第二定律和万有引力定律: ①
解得:
①
解得: .
.
对于A、B两颗粒分别有:  和
和 ,得:
,得: ②
②
(2)设颗粒绕土星作圆周运动的周期为T,则: ③
③
对于A、B两颗粒分别有:  和
和 得:
得:  ④
④
(3)设地球质量为M,地球半径为r0,地球上物体的重力可视为万有引力,探测器上物体质量为m0,在地球表面重力为G0,距土星中心r0/= km处的引力为G
km处的引力为G
 ⑤
⑤  ⑥
⑥
由⑤⑥得: (倍) ⑦
(倍) ⑦
17.(1)由几何关系得:A向右移动 =
=
拉力F1做功: =5.0 J
=5.0 J
(2)设细绳与竖直方向的夹角为 ,因绳不可伸长,所以:vBcos
,因绳不可伸长,所以:vBcos =vAsin
=vAsin
则
vA1=vBcot 1=
1= m/s
m/s
vA2=vBcot 2=
2= m/s
m/s
拉力F2做功:w 2=mBg h+(
h+( )
)
代入数据解得: w2=3.8J
 18.⑴ 减速运动,到右端时速度,
18.⑴ 减速运动,到右端时速度, m/s=
m/s=
包的落地点距B端的水平距离为
s=vt=v =2×
=2× m=
m=
⑵由题意, ω值的范围是ω≤10rad/s.
ω值的范围是ω≤10rad/s.
当ω1=40 rad/s时 ,包的落地点距B端的水平距离为s1==Rωt=v =
=
⑶见图
19.(1)由功能关系, ①
①
 =
=
 =20 碰撞次数为20次,最后球停在C点
=20 碰撞次数为20次,最后球停在C点
(2)设刚好球B能做完整的圆周运动,并设其在最高点的速度为v1,在最低点的速度为v2
 ③
③
 ④
④
 ⑤
⑤
联立③④⑤并代入数据,得L≤
再由②式得最后停在C点右侧
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com