练习册

  • 练习册
  • 试题
    2． , 3．(提示:设.则将代入双曲线方程得.), 4．(提示:到AB的距离之和为8.) [例题探究] 例1．解析设P点的坐标为.则由方程得.A.B两点的坐标分别为又 即.又直线与椭圆交于两点.所以所以点P的轨迹方程为. 例2．解析(1).又.从而.所以 点在以A.B为焦点.长半轴.半焦距.短半轴的椭圆上.曲线E的方程为 (2)设直线.代入E的方程.消.可得所以有解之得设的中点为两点的坐标分别为..将得所以即为M点的轨迹方程. 例3．解析(1)由右准线设则由.得且.=.故有.即为所求点的轨迹G的方程. (2)当.即时.轨迹G是焦点在平行于轴的直线上的椭圆.设其焦点,则消去得 (3)当.即时.轨迹G为圆.其方程为:即又的右准线即 圆心G到准线的距离为此时G与相交. 例4．解析:(1)直线过点.当斜率存在时.设其斜率为.则的方程为记由题设可得点A.B的坐标是方程组的解.消去得于是.设点P的坐标为.则 消去参数得 ①当不存在时.A.B中点为坐标原点(0.0).也满足方程①.所以点P的轨迹方程为. (1) 由点P的轨迹方程知即 又故 当时.取得最小值为, 当时.取得最大值为. [冲刺强化训练18] 【查看更多】

     

    题目列表(包括答案和解析)

    某工厂要建造一个长方体无盖蓄水池，其容积为4800 m3，深3 m．如果池底每1 m2的造价为150元，池壁每1 m2的造价为120元，问怎样设计水池能使总造价最低，最低造价是多少元？(提示：设水池底面一边的长度为x m，总造价为y)

    查看答案和解析>>

    (1)数列{an}和{bn}满足an＝(b1＋b2＋…＋bn)(n=1，2，3…)，求证{bn}为等差数列的充要条件是{an}为等差数列．(8分)

    (2)数列{an}和{cn}满足cn＝an＋2an＋1(nN*)，探究{an}为等差数列的充分必要条件，需说明理由．[提示：设数列{bn}为bn＝an－an＋2(n＝1，2，3…)]

    查看答案和解析>>

    设函数f（x）=（x2+ax+b）ex（x∈R）．
    （1）若a=2，b=-2，求函数f（x）的极值；
    （2）若x=1是函数f（x）的一个极值点，试求出a关于b的关系式（即用a表示b），并确定f（x）的单调区间；（提示：应注意对a的取值范围进行讨论）
    （3）在（2）的条件下，设a＞0，函数g（x）=（a2+14）ex+4．若存在ξ1，ξ2∈[0，4]使得|f（ξ1）-g（ξ2）|＜1成立，求a的取值范围．

    查看答案和解析>>

    设C1，C2，…，Cn，…是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线y=
    		3
    3
    x    相切，对每一个正整数n，圆Cn都与圆Cn+1相互外切，以rn表示Cn的半径，以（λn，0）表示Cn的圆心，已知{rn}为递增数列．
    （1）证明{rn}为等比数列（提示：
    rn
    λn
    =sinθ    ，其中θ为直线y=
    		3
    3
    x    的倾斜角）；
    （2）设r1=1，求数列{
    n
    rn
    }    的前n项和Sn；
    （3）在（2）的条件下，若对任意的正整数n恒有不等式Sn＞
    9
    4
    -
    an
    rn
    成立，求实数a的取值范围．

    查看答案和解析>>

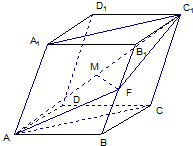    已知四棱柱ABCD-A1B1C1D1中的底面是菱形，且∠DAB=∠A1AB=∠A1AD=60°，AD=1，AA1=a，F为棱BB的中点，M为线段AC的中点．设
    AB
    =
    e1
    ，
    AD
    =
    e2
    ，
    AA1
    =
    e3
    ．试用向量法解下列问题：
    （1）求证：直线MF∥平面ABCD；
    （2）求证：直线MF⊥面A1ACC1；
    （3）是否存在a，使平面AFC1与平面ABCD所成二面角的平面角是30°？如果存在，求出相应的a 值，如果不存在，请说明理由．（提示：可设出两面的交线）

    查看答案和解析>>


    同步练习册答案