
题目列表(包括答案和解析)
解:能否投中,那得看抛物线与篮圈所在直线是否有交点。因为函数![]() 的零点是-2与4,篮圈所在直线x=5在4的右边,抛物线又是开口向下的,所以投不中。
的零点是-2与4,篮圈所在直线x=5在4的右边,抛物线又是开口向下的,所以投不中。
某城市出租汽车的起步价为10元,行驶路程不超出4km,则按10元的标准收租车费![]() 若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,
若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,
(1)他收旅客的租车费η是否也是一个随机变量?如果是,找出租车费η与行车路程ξ的关系式;
(2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?这种情况下,停车累计时间是否也是一个随机变量?
命题“若![]() ,
,![]()
![]() ,
,![]()
![]() ,则
,则![]()
![]() .”可以如下证明:构造函数
.”可以如下证明:构造函数![]() ,则
,则![]() ,因为对一切
,因为对一切![]() ,恒有
,恒有![]() ,所以
,所以![]() ,故得
,故得![]()
![]() .
.
试解决下列问题:
(1)若![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,求证
,求证![]()
![]() ;
;
(2)试将上述命题推广到n个实数,并证明你的结论.
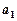 ,
,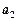
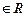 ,
,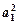
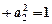 ,则
,则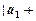
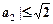 .”可以如下证明:构造函数
.”可以如下证明:构造函数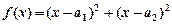 ,则
,则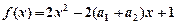 ,因为对一切
,因为对一切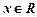 ,恒有
,恒有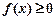 ,所以
,所以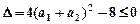 ,故得
,故得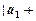
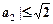 .
.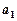 ,
,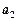 ,
,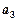
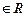 ,
,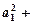
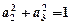 ,求证
,求证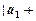
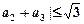 ;
;如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

设人的某一特征(如眼睛大小)是由他一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性.纯显性与混合性的都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子有显性决定特征的概率是多少?
(2)2个孩子中至少有一个显性决定的特征的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com