
题目列表(包括答案和解析)

(2)一条直线和一个平面相交,但不______时,这条直线就叫做这个平面的_______,斜线与平面的交点叫做_____.从平面外一点向平面引斜线,这点与________间的线段叫做这点到这个平面的_______.如图所示,直线PR∩α=R,PR不______于α,直线PR是α的一条_____,点R为_______,线段_____是点P到α的______.?
(3)平面外一点到这个平面的垂线段______条,而这点到这个平面的______有无数条.?
(4)从斜线上斜足以外的一点向平面引垂线,过垂足的直线叫做斜线在这个平面内的_______,________与________间的线段叫做这点到平面的斜线段在这个平面内的________.如图所示,直线_____是直线PR在平面α上的______,线段______是点P到平面α的斜线段PR在平面α上的射影.?
(5)斜线上任意一点在平面上的射影一定在斜线的_____上.事实上,设a是平面α的斜线,B为斜足,在a上任取一点A,作AA1⊥α,A1是垂足,则A1、B确定的直线a′是a在平面α内的______,如图所示,设P是a上任意一点,在a和AA1确定的平面内,作PP1∥AA1,PP1必与a′相交于一点P1.∵AA1α__________ ,PP1______________AA1,∴PP1__________α.P1为P在平面α上的射影,所以点P在平面α上的射影一定在直线a在平面α上的射影a′上.

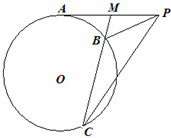
 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
|
| π |
| 6 |
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |
|
| π |
| 6 |
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
A
B
D
B
B
C
B
A
C
D
二.填空题
13. 4 ;
14. ; 15. 2 ; 16.32 ;
; 15. 2 ; 16.32 ;
三.解答题.
17.解:(1) ……………………………2分
……………………………2分
 ……………………………4分
……………………………4分
 …………………………………………6分
…………………………………………6分
(2) 由余弦定理得:
由余弦定理得:
 (当且仅当
(当且仅当 时等号成立)………………9分
时等号成立)………………9分
 …………………………………………………11分
…………………………………………………11分
 的面积最大值为
的面积最大值为 …………………………………………………………12分
…………………………………………………………12分
18.解:(Ⅰ)由 得
得
 …………………2分
…………………2分
∴ ……………………………………4分
……………………………………4分
(Ⅱ)由 整理得
整理得
∴数列 是以
是以 为首项,以2为公比的等比数列, …………………6分
为首项,以2为公比的等比数列, …………………6分
∴
∴
∵当 时
时 满足
满足 ………………………………………8分
………………………………………8分
(Ⅲ)


则 ………………………………………………………………10分
………………………………………………………………10分
∴
∴当 时,
时, ,当
,当 时,
时,
高三数学(理科)(模拟一)答案第1页
即当 或2时,
或2时, 。当
。当 时,
时, ……2分
……2分
19.解:(Ⅰ)掷出点数x可能是:1,2,3,4.
则 分别得:
分别得: 。于是
。于是 的所有取值分别为:0,1,4 .
的所有取值分别为:0,1,4 .
因此 的所有取值为:0,1,2,4,5,8. …………………………………………2分
的所有取值为:0,1,2,4,5,8. …………………………………………2分
当 且
且 时,
时, 可取得最大值8,
可取得最大值8,
此时, ; ………………………………………………………4分
; ………………………………………………………4分
当 时且
时且 时,
时, 可取得最小值 0.
可取得最小值 0.
此时 …………………………………………………………6分
…………………………………………………………6分
(Ⅱ)由(1)知 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
 ……………………………………………………………7分
……………………………………………………………7分
当 时,
时, 的所有取值为(2,3)、(4,3)、(3,2),(3,4)即
的所有取值为(2,3)、(4,3)、(3,2),(3,4)即 ;
;
当 时,
时, 的所有取值为(2,2)、(4,4)、(4,2),(2,4)即
的所有取值为(2,2)、(4,4)、(4,2),(2,4)即 …8分
…8分
当 时,
时, 的所有取值为(1,3)、(3,1)即
的所有取值为(1,3)、(3,1)即 ;
;
当 时,
时, 的所有取值为(1,2)、(2,1)、(1,4),(4,1)即
的所有取值为(1,2)、(2,1)、(1,4),(4,1)即 …9分
…9分
所以 的分布列为:
的分布列为:

0
1
2
4
5
8







…
…………10分
即 的期望
的期望 ………………12分
………………12分
 20.解:(Ⅰ)因为
20.解:(Ⅰ)因为 平面
平面 ,
,
所以平面 平面
平面 ,………………1分
,………………1分
又 ,所以
,所以 平面
平面 ,
,
得 ,又
,又 ………2分
………2分
所以 平面
平面 ; ………………………3分
; ………………………3分
(Ⅱ)因为 ,所以四边形
,所以四边形 为菱形,
为菱形,
故 ,
,
又D为AC中点,知 ……………4分
……………4分
取 中点F,则
中点F,则 平面
平面 ,从而平面
,从而平面 平面
平面 ………………6分
………………6分
过 作
作 于
于 ,则
,则 面
面 ,
,
高三数学(理科)(模拟一)答案第2页
在 中,
中, ,故
,故 ……………………………7分
……………………………7分
即 到平面
到平面 的距离为
的距离为 …………………………………………8分
…………………………………………8分
(Ⅲ)过 作
作 于
于 ,连
,连 ,则
,则
从而 为二面角
为二面角 的平面角, ……………………………………9分
的平面角, ……………………………………9分
在 中
中 ,所以
,所以
在 中,
中, ………………………………………11分
………………………………………11分
故二面角 的大小为
的大小为 ………………………………………12分
………………………………………12分
解法2:(Ⅰ)如图,取AB的中点E,则DE//BC,因为
 所以
所以 又
又 平面
平面 …………………1分
…………………1分
以 为
为 轴建立空间坐标系,
轴建立空间坐标系,
则

 ……………………2分
……………………2分
 由
由 知
知
又 从而
从而 平面
平面 ……………3分
……………3分
(Ⅱ)由 ,得
,得  ………4分
………4分
设平面 的法向量为
的法向量为
所以 设
设 则
则 ……………………………7分
……………………………7分
所以点 到平面
到平面 的距离
的距离 ………………………………8分
………………………………8分
(Ⅲ)再设平面 的法向量为
的法向量为
所以 …………………………………9分
…………………………………9分
故 ,根据法向量的方向, ………………………11分
,根据法向量的方向, ………………………11分
可知二面角 的大小为
的大小为 ………………………………………12分
………………………………………12分
高三数学(理科)(模拟一)答案第3页
21.解:(1)∵ 的图象关于原点对称,∴
的图象关于原点对称,∴ 恒成立,即
恒成立,即
∴ 又
又 的图象在
的图象在 处的切线方程为
处的切线方程为 即
即 …2分
…2分
∴ ,且
,且 而
而 ∴
∴ …………………3分
…………………3分
∴ 解得
解得 故所求的解析式为
故所求的解析式为 ……6分
……6分
(2)解 得
得 或
或
又 ,由
,由 得
得 且当
且当 或
或 时,
时, ………………………………………………………………………………8分
………………………………………………………………………………8分
当 时
时 ∴
∴ 在
在 和
和 递增;在
递增;在 上递减。…9分
上递减。…9分
∴ 在
在 上的极大值和极小值分别为
上的极大值和极小值分别为
而 故存在这样的区间
故存在这样的区间 其中一个区间为
其中一个区间为 …12分
…12分
22. 解:(1)由题意得 设
设
则
由 即
即 ① …………………………………2分
① …………………………………2分
又 在双曲线上,则
在双曲线上,则 ②
②
联立①、②,解得:
由题意, ∴
∴ ∴点T的坐标为(2,0). ………………………………4分
∴点T的坐标为(2,0). ………………………………4分
(2)设直线 与
与 的交点M的坐标为
的交点M的坐标为
由 、P、M三点共线,得:
、P、M三点共线,得: ①
①
由 、
、 、
、 三点共线,得:
三点共线,得: ②
②
联①、②立,解得: ……………………………………………6分
……………………………………………6分
∵ 在双曲线上,∴
在双曲线上,∴
∴轨迹E的方程为 ………………………………………8分
………………………………………8分
高三数学(理科)(模拟一)答案第4页
(3)容易验证直线 的斜率不为0.
的斜率不为0.
故要设直线 的方程为
的方程为 代入
代入 中得:
中得:
设 且
且 ,则由根与系数的关系,
,则由根与系数的关系,
得: ,①
,①  ② ………………………………10分
② ………………………………10分
∵ ,∴有
,∴有 且
且 。将①式平方除以②式,得:
。将①式平方除以②式,得:

由
 ……………………………………………………………12分
……………………………………………………………12分
∵ ∴
∴
又 ∴
∴
故

令 ∵
∵ ∴
∴ 即
即
∴
而 ∴
∴ ∴
∴  …………………14分
…………………14分
高三数学(理科)(模拟一)答案第5页
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com