解析　(1)设木板第一次上升过程中，物块的加速度为a_物块，由牛顿第二定律kmgsin θ－mgsin θ＝ma_物块

解得a_物块＝(k－1)gsin θ，方向沿斜面向上

(2)设以地面为零势能面，木板第一次与挡板碰撞时的速度大小为v₁

由机械能守恒得：×2mv＝2mgH

解得v₁＝

设木板弹起后的加速度为a_板，由牛顿第二定律得：

a_板＝－(k＋1)gsin θ

木板第一次弹起的最大路程s₁＝＝

木板运动的路程s＝＋2s₁＝

(3)设物块相对木板滑动距离为L

根据能量守恒mgH＋mg(H＋Lsin θ)＝kmgLsin θ

摩擦力对木板及物块做的总功W＝－kmgLsin θ

解得W＝－

答案　(1)(k－1)gsin θ；方向沿斜面向上

(2)　(3)－

【解析】（1）电动机的输出功率为W 

F_安=BIL=

当速度稳定时，由平衡条件得

解得v=2m/s 

（2）由能量守恒定律得  

解得t=1s

已知A、B两物块的质量分别为m和3m，用一轻质弹簧连接，放在光滑水平面上，使B物块紧挨在墙壁上，现用力推物块A压缩弹簧（如图所示）．这个过程中外力F做功为W，待系统静止后，突然撤去外力．在求弹簧第一次恢复原长时A、B的速度各为多大时，有同学求解如下：

解：设弹簧第一次恢复原长时A、B的速度大小分别为v_A、v_B

系统动量守恒：0=mv_A＋3mv_B

系统机械能守恒：W=

解得：；（“－”表示B的速度方向与A的速度方向相反）

（1）你认为该同学的求解是否正确．如果正确，请说明理由；如果不正确，也请说明理由并给出正确解答．

（2）当A、B间的距离最大时，系统的弹性势能E_P=？

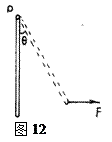
如图12所示粗细均匀的木棒长为L，质量为M ，可绕固定转动轴O自由转动，现用水平力F作用于木棒的下端将木棒从竖直位置缓慢拉起，并转过θ角度，则在拉起的过程中，拉力F做的功为多少？

 某同学解法为：

木棒与竖直位置成θ时，木棒所受的力矩平衡   Mg Lsinθ/2= F Lcosθ，

得到F=Mgtgθ/2

从竖直位置缓慢拉起的过程中，  拉力F从0变化到Mgtgθ/2，

拉力F的平均值=Mgtgθ/4          

拉力作用点在力F方向上的位移是    S=L sinθ

根据W=FS     解得 ：拉力F 做的功：W_F= Mg L sinθtgθ/4

所以在拉起的过程中，拉力F做的功为W_F=Mg L sinθtgθ/4 ，

你认为他的解法是否正确？若正确，请说明理由；若错误，也请说明理由，并且解出正确的结果。