
题目列表(包括答案和解析)
已知曲线C: (m∈R)
(m∈R)
(1) 若曲线C是焦点在x轴点上的椭圆,求m的取值范围;
(2) 设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证:A,G,N三点共线。
【解析】(1)曲线C是焦点在x轴上的椭圆,当且仅当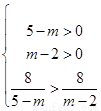 解得
解得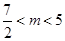 ,所以m的取值范围是
,所以m的取值范围是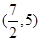
(2)当m=4时,曲线C的方程为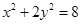 ,点A,B的坐标分别为
,点A,B的坐标分别为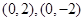 ,
,
由 ,得
,得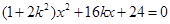
因为直线与曲线C交于不同的两点,所以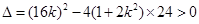
即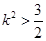
设点M,N的坐标分别为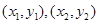 ,则
,则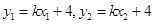
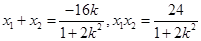
直线BM的方程为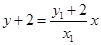 ,点G的坐标为
,点G的坐标为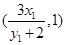
因为直线AN和直线AG的斜率分别为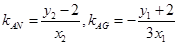
所以
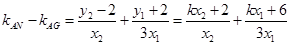
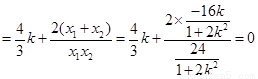
即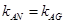 ,故A,G,N三点共线。
,故A,G,N三点共线。
已知函数 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
【解析】本试题考查了三角函数的图像与性质的运用。第一问中,利用 可知函数的周期为
可知函数的周期为 ,最大值为
,最大值为 。
。
第二问中,函数 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。
第三问中,利用图像将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的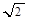 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
解:(1)函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 。
。
(2)函数 的单调区间与函数
的单调区间与函数 的单调区间相同。
的单调区间相同。
 即
即
 所求的增区间为
所求的增区间为 ,
,
 即
即
 所求的减区间为
所求的减区间为 ,
, 。
。
(3)将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的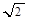 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
已知 中,
中, ,
, .设
.设 ,记
,记 .
.
(1) 求 的解析式及定义域;
的解析式及定义域;
(2)设 ,是否存在实数
,是否存在实数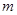 ,使函数
,使函数 的值域为
的值域为 ?若存在,求出
?若存在,求出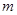 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用(1)如图,在 中,由
中,由 ,,
,,
可得 ,
,
又AC=2,故由正弦定理得

(2)中
由 可得
可得

 .显然,
.显然, ,则
,则
1 当m>0的值域为
当m>0的值域为
 m+1=3/2,n=1/2
m+1=3/2,n=1/2
2 当m<0,不满足
当m<0,不满足 的值域为
的值域为 ;
;
因而存在实数m=1/2 的值域为
的值域为 .
.
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
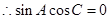

又由 得
得 即
即

又由 得
得 即
即

又
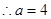 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

已知向量 =(
=( ),
), =(
=(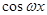 ,
,
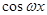 ),其中(
),其中(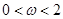 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 .
.
(I)求函数 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
【解析】第一问利用向量的数量积公式表示出
 ,然后利用
,然后利用 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
解:因为

由余弦定理得 ,……11分故
,……11分故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com