题目列表(包括答案和解析)
某超市在节日期间进行有奖促销，凡在该超市购物满300元的顾客，将获得一次摸奖机会，规则如下：
奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就要将奖盒中的球全部摸出才停止．规定摸到红球奖励10元，摸到白球或黄球奖励5元，摸到黑球不奖励．
（Ⅰ）求1名顾客摸球3次停止摸奖的概率；
（Ⅱ）记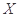
为1名顾客摸奖获得的奖金数额，求随机变量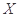的分布列和数学期望．
（08年新建二中二模理）小张有一只放在
个红球,
个黄球,
个白球的箱子,且
.小刘有一只放有
个红球,
黄球,
个白球的箱子,两人各自从自己的箱子中任取一球,规定：当两球同 色时小张胜,异色时小刘胜.
⑴用
表示小张获胜的概率；
⑵若又规定当小张取红、黄、白球而胜得分分别为分、分、分,否则得
分,求小张得分的期望的最大值及此时的值.
某超市在节日期间进行有奖促销，凡在该超市购物满300元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就要将奖盒中的球全部摸出才停止．规定摸到红球奖励10元，摸到白球或黄球奖励5元，摸到黑球不奖励．
（Ⅰ）求1名顾客摸球3次停止摸奖的概率；
（Ⅱ）记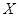
为1名顾客摸奖获得的奖金数额，求随机变量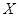的分布列和数学期望．
注意事项：
１．本试卷满分150分，考试时间120分钟.
２．答卷前，考生务必将自己的学校、班级、姓名等写在三相应的位置．
３．本卷为答题卷，要求将所有试题答案或解答写在答题卷指定位置上．
４．请用
考 生 填 写 座 位
号 码 的 末 两 位
题 号
一
二
三
四
17
18
19
20
21
22
23
得 分
一．选择题：(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的;每小题选出答案后，请用2B铅笔把就机读卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
C
D
C
C
B
D
B
A
A
得分
评卷人
二．填空题(请把答案填在对应题号的横线上)
13. 
. 14．
.
15．
. 16. 
.
三.解答题（本大题共5小题，共64分.解答应写出文字说明、证明过程或演算步骤.请将答题的过程写在答题卷中指定的位置.）
17.( 本题满分12分)
解：（Ⅰ）∵
，∴ 
（3分），又∵ 
是钝角，
∴ 
（或
）；...............6分
（Ⅱ）由余弦定理得，
，..........9分
∴ 
.................12分，
18．（本题满分12分）
解：（Ⅰ）设两个红球为
，三个白球为
，从中任意选取2个球，所有可能的结果如下：（），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
），（
）共有20种，………………………………………………………（5分）
其中红球、白球都有的结果是（），（），（），（），（），（），（），（），（），（），（），（）共有12种，
所以红球、白球都有的概率为
；…（8分）
（Ⅱ）∵“红球个数不少于白球个数”包含两类：两红，一红一白，
∴由（Ⅰ）知中奖的概率为
．……………………（12分）
19．（本题满分12分）
证明：（Ⅰ）∵ 
∥
，
又
，
，
∴ ∥
；........4分
（Ⅱ）在三棱柱
中，
∵ 
，
∴ 四边形
，
，
都是矩形，
又 ∵ 
，
，
，
∴ 
，又 ∵ 
为
中点，
在
中，
，同理，
．
∴ 
，∴ 
，.....8分
在
中，
，
在
中，
，
∴ 
，∴ 
．....10分
又 
，
∴ 
．..........12分
解法二：（Ⅱ）以
为原点，建立如图所示的空间直角坐标系，设
，
，
，
（6分），则 
，
，
，
∴ 
，
∴
，∴
（8分），
∴ 
，
∴ 
，∴（10分）
又 
，∴ ．....12分
20.（本题满分14分）
解；（Ⅰ）设圆
：
....①，将
和
两点坐标代入①得，
........................②（2分）
又 ∵ 圆心
在直线
上，则 
...........③（3分）
联立②、③解之
（4分），将代入
中，得 
，
故 圆的方程为 
（5分）．
（Ⅱ）∵直线
与
的倾斜角互补，又点在圆上，且
为圆上相异两点，∴ 它们的倾斜角都不为
，∴它们的斜率互为相反数（6分），
设直线的方程为 
，则直线的方程为
（7分），
联立 
，.............（9分）
（或 
（9分））
解之：
，
，
（11分），
（或 解之
，
（11分））
同理可得，
，
（12分），
（或 
（12分））
∴ 
............14分
（或
...........14分）
21.（本题满分14分）
解：（Ⅰ）当
=
9时
则
......2分
令
解得：
或
........3分
故函数
在区间（－
，－１）上是增函数，
在区间（３，＋）上也是增函数．..5分
（Ⅱ）
函数
在（－，＋）上为增函数，∴对于
，
０恒成立，
故：
＝36－12
0，解得：3.........8分
所以3时，函数在（－，＋）上为增函数．......9分
（Ⅲ）在（Ⅱ）条件下函数在（－，＋）上为增函数，所以， 函数在区间
上是增函数，故有：
，∵
，∴
，从而方程x=至少有两个不相等的实数根，即方程
至少有两个不相等的实数根．.............11分
又方程有一根为0，故：方程
至少有一个不为0的根.
∴
，解得：
且
0............13分
又∵3
∴ ３．...........14分
四．选考题(从下列两道解答题中任选一道作答，作答时，请注明题号；若多做，则按首做题计入总分，满分10分; 请将答题的过程写在答题卷中指定的位置）
你选做_______题(请在横线上注明题号)
解（或证明）：
22. 证明：∵是
的切线，直线
是的割线
∴ 
，（2分）
又 ∵ 
，∴
，∴ 
（5分），
∵ 
，
∴ △
与△
两边对应成比例，且夹角相等（7分），
∴ △∽△（8分）
∴ 
（10分）．
23. 解：（Ⅰ）直线
的参数方程是
，即 
..5分
（Ⅱ）设
，则
，
∵
，
（7分），
∴ 
，即圆的极坐标方程为
．.........10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com