练习册

  • 练习册
  • 试题
    吉林省延边州2008-2009学年度质量检测 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题12分）试用含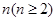的表达式表示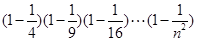的值，并用数学归纳法证明你的结论.

     

    查看答案和解析>>

    （本小题12分）
    已知是等差数列，且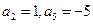
    ①求的通项。
    ②求的前n项和Sn的最大值。

    查看答案和解析>>

    (本小题12分)

    已知,

     (1)判断的奇偶性并用定义证明；

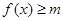    (2)当时，总有成立，求的取值范围.

     

    查看答案和解析>>

    （本小题12分）若数列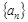的前n 项和Sn满足：Sn= 2an+1.

    （1）求，，；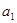

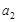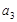    （2）求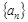的通项公式.

     

    查看答案和解析>>

    （本小题12分）袋中有大小、形状相同的红、黑球各两个，现依次不放回地随机取3次，每次取一个球.

    （1）试问：一共有多少种不同的结果，请列出所有可能的结果；

    （2）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率.

     

    查看答案和解析>>

    一.选择题:

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    B

    D

    A

    D

    C

    D

    A

    C

    B

    A

    C

    B

    二.填空题:

    13. 7 ;14.;15. ;16①②③④

    三.解答题:

    18. 记第一、二、三次射击命中目标分别为事件A，B，C三次均未命中目标的事件为D．依题意． 设在处击中目标的概率为，则，由

    时，所以，， 2分   ，

    ，，．

    5 分

    （Ⅰ）由于各次射击都是独立的，所以该射手在三次射击击中目标的概率为

    ，

    ＝．  8分

     

    （Ⅱ）依题意，设射手甲得分为，则，，

    ，，所以的分布列为

    ０

    １

    ２

    ３

    所以。    12分

     

     

     

    20. （Ⅰ）证明：连结交于点，连结.

    在正三棱柱中，四边形是平行四边形，

    ∴.

    ∵，

    ∴∥.   ………………………2分

          ∵平面，平面，

    ∴∥平面.       …………………………4分

     

    (Ⅱ）过点作交于，过点作交于，连结.

    ∵平面平面，平面，平面平面，

          ∴平面.

    ∴是在平面内的射影.

    ∴.

    ∴是二面角的平面角.  

    在直角三角形中，.

    同理可求： .

    ∴.

    ∵，

    ∴.   …………………………12分

     

    21.（Ⅰ），令，解得或，1分   

    当时，，为增函数；当时，为减函数；当时，为增函数。4分  当时，取得极大值为-4，当时，取处极小值为。…………………………6分

    （Ⅱ）设，在上恒成立.

    ,,若,显然。 8分   若,

    ,令,解得,或,当时,

    ,当时,.10分  

     当时,.

    即,解不等式得,,当时,

    满足题意.综上所述的范围为…………...12分

     

     

     


    同步练习册答案