
题目列表(包括答案和解析)
已知两点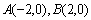 ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为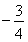 .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆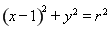 (
(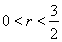 )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值(其中点O为坐标原点).
已知两点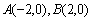 ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为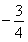 .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆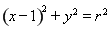 (
(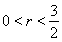 )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值(其中点O为坐标原点).
如图,平面ABDE⊥平面ABC,AC BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD AE,BD
AE,BD BA,AE=2BD=4,O、M分别为CE、AB的中点.
BA,AE=2BD=4,O、M分别为CE、AB的中点.
(Ⅰ)证明:OD//平面ABC;
(Ⅱ)能否在EM上找一点N,使得ON⊥平面ABDE?若能,请指出点N的位置,并加以证明;若不能,请说明理由.

【解析】第一问:取AC中点F,连结OF、FB.∵F是AC的中点,O为CE的中点,
∴OF∥EA且OF= 且BD=
且BD=
∴OF∥DB,OF=DB,
∴四边形BDOF是平行四边形。
∴OD∥FB
第二问中,当N是EM中点时,ON⊥平面ABDE。 ………7分
证明:取EM中点N,连结ON、CM, AC=BC,M为AB中点,∴CM⊥AB,
又∵面ABDE⊥面ABC,面ABDE 面ABC=AB,CM
面ABC=AB,CM 面ABC,
面ABC,
∴CM⊥面ABDE,∵N是EM中点,O为CE中点,∴ON∥CM,
∴ON⊥平面ABDE。
已知两点 ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为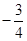 .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆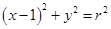 (
(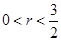 )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值(其中点O为坐标原点).
已知两点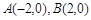 ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为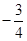 .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆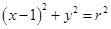 (
(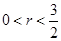 )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值(其中点O为坐标原点).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com